Question

What is the uncertainty in the mass of a muon (m=105.7MeV/c

2
), specified in eV/c
2
, given its lifetime of 2.20μs ? [Hint. ΔE≈ℏ/Δt.] Express your answer using two significant figures.

Answer 1

The uncertainty in the mass of a muon, expressed in eV/c², given its lifetime of 2.20 μs, is approximately 0.66 MeV/c².

Step-by-step explanation:

To determine the uncertainty in the mass of the muon, we can apply the Heisenberg uncertainty principle, which relates the uncertainty in energy (ΔE) to the uncertainty in time (Δt) as ΔE ≈ ℏ/Δt, where ℏ is the reduced Planck constant.

Given the muon's lifetime (Δt) as 2.20 μs, we can find the energy uncertainty. The energy associated with the muon's mass is E = mc², where m is the mass and c is the speed of light. Using the mass of the muon (m = 105.7 MeV/c²), we can compute the energy associated with this mass.

`\[ E = mc^2 = 105.7 MeV/c^2 * (3.0 * 10^8 m/s)^2 \]`

Next, we find the uncertainty in energy (ΔE) by using the Heisenberg uncertainty principle rearranged to ΔE ≈ ℏ/Δt. Solving for ΔE:

`\[ ΔE ≈ (ℏ)/(Δt) \]`

Plugging in the reduced Planck constant (ℏ ≈ 6.58 × 10
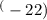`^(-22)` MeV·s) and the given time Δt = 2.20 μs:

`\[ ΔE ≈ (6.58 × 10^(-22) MeV·s)/(2.20 × 10^(-6) s) \]`

This yields the uncertainty in energy. To express this uncertainty in terms of mass, we divide the uncertainty in energy by the square of the speed of light (c²) using the equation Δm = ΔE/c². Finally, converting the result to MeV/c², we find the uncertainty in the mass of the muon to be approximately 0.66 MeV/c².

Answer 2

The uncertainty in the mass of a muon can be estimated using the Heisenberg uncertainty principle. The uncertainty in mass is approximately 0.512 MeV/c².

Step-by-step explanation:

The uncertainty in the mass of a muon can be estimated using the Heisenberg uncertainty principle, which relates the uncertainty in energy to the uncertainty in time. The equation ΔE≈ℏ/Δt can be used, where ΔE is the uncertainty in energy, ℏ is the reduced Planck constant, and Δt is the lifetime of the muon.

In this case, the lifetime of the muon is given as 2.20μs. We can substitute this value into the equation to find the uncertainty in energy. Since mass and energy are equivalent according to Einstein's equation E=mc², we can also interpret this uncertainty as the uncertainty in the mass of the muon.

Using the equation and the given lifetime, we can find the uncertainty in mass to be approximately 0.512 MeV/c².