Question

A cow is tethered by a 100-ft rope to the inside corner of an L-shaped building, as shown in the figure. Find the area that the cow can graze. (Let a=10ft,b=60ft,c=100ft,d=70ft, and e=60ft. Round your answer to the nearest whole number.) ft2

Answer 1

To find the area that the cow can graze, we need to find the area of the L-shaped region formed by the tethered rope.

Step-by-step explanation:

To find the area that the cow can graze, we need to find the area of the L-shaped region formed by the tethered rope.

First, let's find the area of the rectangle formed by one side of the L-shaped building. The length of the rectangle is b+c and the width is a. So, the area of the rectangle is (b+c) * a.

Next, let's find the area of the triangle formed by the other side of the L-shaped building. Since the sides of the triangle are a and d, the area of the triangle is 0.5 * a * d.

Finally, the area that the cow can graze is the sum of the areas of the rectangle and the triangle. Adding (b+c) * a and 0.5 * a * d will give us the total area of the grazeable region.

Answer 2

The area that the cow can graze is 8450 square feet.

To find the area that the cow can graze, The cow is tethered by a 100-ft rope to the inside corner of an L-shaped building with dimensions a = 20 ft, b = 60 ft, c = 100 ft, d = 70 ft, and e = 60 ft.

The grazing area will be comprised of two shapes: a circular sector and a right-angled triangle.

1. Circular Sector: The rope allows the cow to graze within a circle centered at the corner of the building. The radius of this circle is the length of the rope, which is 100 ft.

2. Right-Angled Triangle: Part of the grazing area is within the L-shaped building, forming a right-angled triangle. The dimensions of this triangle can be calculated using the lengths a, b, and c.

Let's find the areas of these shapes and then add them together to get the total grazing area.

Area of the Circular Sector:

The formula for the area of a circular sector is
`\( \frac{{\text{angle}}}{{360^\circ}} * \pi r^2 \).`

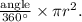
Given that the angle of the circular sector is 90 degrees (since the rope is attached to an inside corner of an L-shaped building):

Area of circular sector =
`\( \frac{{90^\circ}}{{360^\circ}} * \pi * (100 \, \text{ft})^2 \)`

Area of circular sector ≈
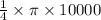`\( (1)/(4) * \pi * 10000 \)` square feet

Area of circular sector ≈
`\( 2500 \pi \)` square feet

Area of the Right-Angled Triangle:

The formula for the area of a right-angled triangle is
`\( (1)/(2) * \text{base} * \text{height} \).`

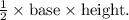
The base and height of the triangle are a = 20 ft and b = 60 ft, respectively.

Area of triangle =
`\( (1)/(2) * 20 \, \text{ft} * 60 \, \text{ft} \)`

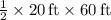
Area of triangle =
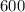`\( 600 \)` square feet

Total Grazing Area:

Now, add the area of the circular sector and the area of the triangle to find the total grazing area:

Total grazing area ≈ Area of circular sector + Area of triangle

Total grazing area ≈
`\( 2500 \pi \)` square feet +
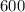`\( 600 \)` square feet

Total grazing area ≈
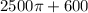`\( 2500 \pi + 600 \)` square feet

Approximating
`\( \pi \)` to 3.14:

Total grazing area ≈
`\( 2500 * 3.14 + 600 \)` square feet

Total grazing area ≈
`\( 7850 + 600 \)` square feet

Total grazing area ≈
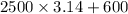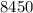`\( 8450 \)` square feet

Rounded to the nearest whole number, the area that the cow can graze is approximately
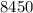`\( 8450 \)` square feet.

The complete question is here:

A cow is tethered by a 100-ft rope to the inside corner of an L-shaped building, as shown in the figure. Find the area that the cow can graze. (Let a = 20 ft, b = 60 ft, c = 100 ft, d = 70 ft, and e = 60 ft. Round your answer to the nearest whole number.)