Question

In ambulance traveling eastbound at 104.0 km/h with sirens blaring at a frequency of 6.00×10

2
Hz passes cars traveling in both the astbound and westbound directions at 57.0 km/h. (Assume the speed of sound is 343 m/s.) (a) What is the frequency observed by the eastbound drivers as the ambulance approaches from behind? Hz (b) What is the frequency observed by the eastbound drivers after the ambulance passes them? Hz (c) What is the frequency observed by the westbound drivers as the ambulance approaches them? Hz (d) What is the frequency observed by the westbound drivers after the ambulance passes them? Hz

Answer 1

The observed frequencies are approximately 624.59 Hz, 578.01 Hz, 579.89 Hz, and 624.21 Hz for scenarios a), b), c), and d) respectively.

Calculate the observed frequencies using the Doppler effect formulas.

Given:

- Emitted frequency (f) = 600 Hz

- Speed of sound (v) = 343 m/s

- Velocity of the ambulance
`(\( v_s \)) = 104.0 km/h = 28.9 m/s`

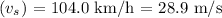
- Velocity of the cars
`(\( v_o \)) = 57.0 km/h = 15.8 m/s`

a) Frequency observed by the eastbound drivers as the ambulance approaches:

Using the formula for approaching:

`\[ f' = f \cdot \left( (v + v_o)/(v + v_s) \right) \]`

`\[ f' = 600 \, \text{Hz} \cdot \left( \frac{343 \, \text{m/s} + 15.8 \, \text{m/s}}{343 \, \text{m/s} + 28.9 \, \text{m/s}} \right) \]`

`\[ f' \approx 624.59 \, \text{Hz} \]`

b) Frequency observed by the eastbound drivers after the ambulance passes them:

After the ambulance passes, the formula changes slightly to:

`\[ f' = f \cdot \left( (v - v_o)/(v - v_s) \right) \]`

`\[ f' = 600 \, \text{Hz} \cdot \left( \frac{343 \, \text{m/s} - 15.8 \, \text{m/s}}{343 \, \text{m/s} - 28.9 \, \text{m/s}} \right) \]`

`\[ f' \approx 578.01 \, \text{Hz} \]`

c) Frequency observed by the westbound drivers as the ambulance approaches them:

When approaching, for the westbound drivers:

`\[ f' = f \cdot \left( (v + v_o)/(v - v_s) \right) \]`

`\[ f' = 600 \, \text{Hz} \cdot \left( \frac{343 \, \text{m/s} + 15.8 \, \text{m/s}}{343 \, \text{m/s} - 28.9 \, \text{m/s}} \right) \]`

`\[ f' \approx 579.89 \, \text{Hz} \]`

d) Frequency observed by the westbound drivers after the ambulance passes them:

After the ambulance passes, for the westbound drivers:

`\[ f' = f \cdot \left( (v - v_o)/(v + v_s) \right) \]`

`\[ f' = 600 \, \text{Hz} \cdot \left( \frac{343 \, \text{m/s} - 15.8 \, \text{m/s}}{343 \, \text{m/s} + 28.9 \, \text{m/s}} \right) \]`

`\[ f' \approx 624.21 \, \text{Hz} \]`

These are the calculated observed frequencies for each scenario based on the given information and the Doppler effect formulas.

Answer 2

(a) The frequency observed by the eastbound drivers as the ambulance approaches from behind is 710.36 Hz.

(b) The frequency observed by the eastbound drivers after the ambulance passes them is 506.8 Hz.

(c) The frequency observed by the westbound drivers as the ambulance approaches them is 658.1 Hz.

(d) The frequency observed by the westbound drivers after the ambulance passes them is 547.1 Hz.

How to calculate the frequency observed?

(a) The frequency observed by the eastbound drivers as the ambulance approaches from behind is calculated as follows;

f = f₀ (v + v₀ ) / (v - v₀)

where;

• f₀ is the frequency of ambulance = 600 Hz
• v is the speed of sound = 343 m/s
• v₀ is the eastbound speed = 104 km/h = 28.89 m/s

f = 600 Hz (343 + 28.89 ) / ( 343 - 28.89)

f = 710.36 Hz

(b) The frequency observed by the eastbound drivers after the ambulance passes them is;

f = f₀ (v - v₀ ) / (v + v₀)

f = 600 Hz (343 - 28.89) / (343 + 28.89)

f = 506.8 Hz

(c) The frequency observed by the westbound drivers as the ambulance approaches them is;

v₀ = 57 km/h = 15.83 m/s

f = f₀ (v + v₀ ) / (v - v₀)

f = 600 Hz (343 + 15.83 ) / ( 343 - 15.83)

f = 658.1 Hz

(d) The frequency observed by the westbound drivers after the ambulance passes them is;

f = f₀ (v - v₀ ) / (v + v₀)

f = 600 Hz (343 - 15.83) / (343 + 15.83)

f = 547.1 Hz