(a) The velocity at the top of the circle is approximately
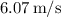 .
.
(b) The tension at the top of the circle is approximately
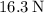 .
.
In a vertical circular motion, the speed of the object changes as it moves around the circle. At the bottom of the circle, the tension in the string provides the centripetal force required for circular motion, and at the top, gravity provides the centripetal force. Let's solve for the velocity at the top and the tension at the top.
Given:
- Mass of the ball
 = 200 g = 0.2 kg
= 200 g = 0.2 kg
- Length of the string
 = 50 cm = 0.5 m
= 50 cm = 0.5 m
- Speed at the bottom
 = 10 m/s
= 10 m/s
First, let's find the velocity at the top
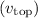 . The conservation of energy can be applied, considering the conversion of potential energy to kinetic energy:
. The conservation of energy can be applied, considering the conversion of potential energy to kinetic energy:
![\[ mgh_{\text{bottom}} + (1)/(2)mv_{\text{bottom}}^2 = mgh_{\text{top}} + (1)/(2)mv_{\text{top}}^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/slx0ygpqrbtvpckf7yxetqpbszc9gdgf3t.png)
At the bottom of the circle,
 (since the reference point is usually at the bottom), and at the top of the circle,
(since the reference point is usually at the bottom), and at the top of the circle,
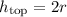 .
.
![\[ (1)/(2)mv_{\text{bottom}}^2 = mg(2r) + (1)/(2)mv_{\text{top}}^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/q59csfnbwwhntmibj5x2njl01yp2idvmr2.png)
Now, solve for
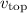 .
.
![\[ v_{\text{top}} = \sqrt{v_{\text{bottom}}^2 - 2gr} \]](https://img.qammunity.org/2024/formulas/physics/high-school/mj29ej0t0uk4j2fc22fp8dpryqerbz9xu4.png)
Substitute the known values:
![\[ v_{\text{top}} = \sqrt{(10 \, \text{m/s})^2 - 2 * 9.8 \, \text{m/s}^2 * 0.5 \, \text{m}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/zg8u29hjrb2l3qf2v2x95x0fjpgu4bqbrb.png)
![\[ v_{\text{top}} \approx 6.07 \, \text{m/s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/3xrzv3xpjriqc0jkk018uby5e34qcliog1.png)
Next, let's find the tension at the top
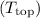 . At the top of the circle, the net force acting on the ball is the centripetal force provided by tension, so:
. At the top of the circle, the net force acting on the ball is the centripetal force provided by tension, so:
![\[ T_{\text{top}} = \frac{mv_{\text{top}}^2}{r} + mg \]](https://img.qammunity.org/2024/formulas/physics/high-school/uksb9i58c4ddt1f9hmcmpsdm07lvdyrslv.png)
![\[ T_{\text{top}} = \frac{0.2 \, \text{kg} * (6.07 \, \text{m/s})^2}{0.5 \, \text{m}} + 0.2 \, \text{kg} * 9.8 \, \text{m/s}^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/5edp5g79zlvvg0ojaiuqkluk04oa2vrsoa.png)
![\[ T_{\text{top}} \approx 16.3 \, \text{N} \]](https://img.qammunity.org/2024/formulas/physics/high-school/hqjx4ppwt8xzfikg9wukp9lmyks9pxxko9.png)