Question

On a space platform, a 125kg robot is standing on a 23m long, 330kg steel beam that is floating in space, motionless relative to the platform and pointing South. Using its magnetic feet it walks along the beam in the Southerly direction at 1.65m/s relative to the beam. What is the robot's velocity relative to the platform in m/s?

Answer 1

The robot's velocity relative to the platform is 1.65m/s in the Southerly direction.

Step-by-step explanation:

The robot's velocity relative to the platform can be calculated by adding its velocity relative to the beam to the velocity of the beam relative to the platform. Since the robot is walking in the Southerly direction at 1.65m/s relative to the beam, and the beam is motionless relative to the platform, the robot's velocity relative to the platform will also be 1.65m/s in the Southerly direction.

Answer 2

The robot's velocity relative to the platform is approximately
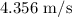`\(4.356 \text{ m/s}\)` in the northern direction.

The total momentum of the system (robot + steel beam) remains constant as there are no external forces acting on it in space. The initial momentum is zero since both objects are motionless relative to the platform.

The mass of the robot is 125 kg, and the mass of the steel beam is 330 kg.

When the robot starts walking along the beam, its velocity relative to the beam is given as 1.65 m/s south.

Let's consider the conservation of momentum.

Initial momentum of the system = Final momentum of the system

The initial momentum is zero since both the robot and the beam are motionless relative to the platform.

The final momentum will be the sum of the momenta of the robot and the beam after the robot starts walking.

Let
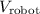`\(V_{\text{robot}}\)` be the velocity of the robot relative to the platform.

The momentum of the robot after it starts walking = Mass of the robot × Velocity of the robot relative to the platform

`\(= 125 \text{ kg} * V_{\text{robot}}\)`

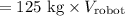
The momentum of the steel beam after the robot starts walking = Mass of the steel beam × Velocity of the robot relative to the beam

`\(= 330 \text{ kg} * 1.65 \text{ m/s}\)`

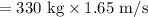
According to the conservation of momentum:

`\[0 = 125 \text{ kg} * V_{\text{robot}} + 330 \text{ kg} * 1.65 \text{ m/s}\]`

Solving for \(V_{\text{robot}}\):

`\[V_{\text{robot}} = - \frac{330 \text{ kg} * 1.65 \text{ m/s}}{125 \text{ kg}}\]`

`\[V_{\text{robot}} \approx -4.356 \text{ m/s}\]`

The negative sign indicates that the robot is moving in the opposite direction to the initial position of the beam relative to the platform.