Question

A uniform, solid sphere of radius 4.50 cm and mass 2.00 kg starts with a purely translational speed of 2.75 m/s at the top of an inclined plane. The surface of the incline is 1.25 mlong and is tilted at an angle of 26.0∘ with respect to the horizontal. Assuming the sphere rolls without slipping down the incline, calculate the sphere's final translational speed 2 at the bottom of the ramp.

2=

Answer 1

The sphere's final translational speed at the bottom of the ramp is approximately 2.98 m/s.

To calculate the sphere's final translational speed at the bottom of the ramp, we can use the principle of conservation of mechanical energy.

The mechanical energy of the system, which includes both kinetic energy (KE) and potential energy (PE), remains constant as long as no external forces are acting on the sphere.

Given:

Radius of the sphere (r) = 4.50 cm = 0.045 m

Mass of the sphere (m) = 2.00 kg

Initial translational speed at the top (v1) = 2.75 m/s

Length of the incline (d) = 1.25 m

Angle of the incline (θ) = 26.0 degrees

First, let's calculate the initial potential energy (PE1) of the sphere at the top of the incline:

PE1 = m * g * h

= m * g * d * sin(θ)

Next, let's calculate the final potential energy (PE2) of the sphere at the bottom of the incline:

PE2 = m * g * h

= m * g * d * sin(0 degrees)

= 0

Since the sphere rolls without slipping, its initial rotational energy is zero. Therefore, the total mechanical energy (E1) at the top is equal to the kinetic energy (KE1):

E1 = KE1 + PE1

`= (1/2) * m * v1^2 + m * g * d * sin(\theta)`

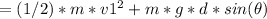
At the bottom of the incline, the mechanical energy (E2) is equal to the final kinetic energy (KE2):

E2 = KE2 + PE2

`= (1/2) * m * v2^2`

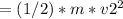
Using the conservation of mechanical energy, we can equate E1 and E2:

`(1/2) * m * v1^2 + m * g * d * sin(\theta) = (1/2) * m * v2^2`

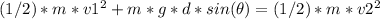
Simplifying the equation:

`v2^2 = v1^2 + 2 * g * d * sin(\theta)`

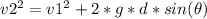
Now, let's substitute the given values into the equation and solve for v2:

`v2^2 = (2.75 m/s)^2 + 2 * (9.8 m/s^2) * (1.25 m) * sin(26.0 degrees)`

`v2^2 = 8.87 m^2/s^2`

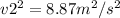
Taking the square root:

v2 ≈ 2.98 m/s

Therefore, the sphere's final translational speed at the bottom of the ramp is approximately 2.98 m/s.

For more question on translational speed visit: