Question

A man pushes a lawn mower with a force of 34lb exerted at an angle of 30

∘
to the ground. Find the horizontal and vertical components of the force. (Assume that th horizontal direction is positive and the vertical direction is negative.) 3

Answer 1

The horizontal component of the force is approximately
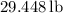`\(29.448 \, \text{lb}\)` and the vertical component of the force is
`\(17 \, \text{lb}\)`.

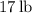To find the horizontal and vertical components of the force, you can use trigonometric functions since the force is exerted at an angle to the ground.

The force exerted by the man is 34 pounds at an angle of 30 degrees to the ground.

The horizontal component of the force can be found using the cosine function:

`\[ \text{Horizontal component} = \text{Force} * \cos(\text{angle}) \]`

`\[ \text{Horizontal component} = 34 \, \text{lb} * \cos(30^\circ) \]`

Cosine of 30 degrees is
`\( \cos(30^\circ) = (√(3))/(2) \)`.

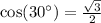So,

`\[ \text{Horizontal component} = 34 \, \text{lb} * (√(3))/(2) \]`

`\[ \text{Horizontal component} \approx 29.448 \, \text{lb} \]`

The vertical component of the force can be found using the sine function:

`\[ \text{Vertical component} = \text{Force} * \sin(\text{angle}) \]`

`\[ \text{Vertical component} = 34 \, \text{lb} * \sin(30^\circ) \]`

Sine of 30 degrees is
`\( \sin(30^\circ) = (1)/(2) \)`.

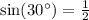So,

`\[ \text{Vertical component} = 34 \, \text{lb} * (1)/(2) \]`

`\[ \text{Vertical component} = 17 \, \text{lb} \]`

Answer 2

The horizontal and vertical components of the force is 29.44 lb and 17 lb respectively.

How to calculate the horizontal and vertical component of the force?

The horizontal and vertical component of the force is calculated by applying the following formula as shown below;

The horizontal component of the force is calculated as;

Fx = F cos(θ)

Fx = 34 lb x cos (30)

Fx = 29.44 lb

The vertical component of the force is calculated as;

Fy = F sin (θ)

Fy = 34 lb x sin (30)

Fy = 17 lb

Thus, the horizontal and vertical components of the force is 29.44 lb and 17 lb respectively.