Question

1. The foreign demand for our exports X depends on the foreign income Y

f
​
and our price level P such that X=Y
f
1/2
​
+P
−2
. Find the partial elasticity of foreign demand for our exports with respect to our price level.

Answer 1

The partial elasticity of foreign demand for our exports with respect to our price level is -1.

Step-by-step explanation:

The given foreign demand function is represented as
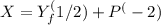`X = Y_f^(1/2) + P^(-2)` , where X is the foreign demand for our exports,
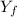`Y_f` is the foreign income, and P is our price level. To find the partial elasticity of foreign demand with respect to our price level (dX/dP), we differentiate the equation with respect to P.

`\[dX/dP = 0 - 2 * P^(-3) = -2/P^3\]`

Now, to find the partial elasticity, we use the formula:

`\[E = (dX/dP) * (P/X)\]`

Substituting the values:

`\[E = (-2/P^3) * (P/(Y_f^(1/2) + P^(-2)))\]`

Simplifying further:

`\[E = -2 * P^(-2) / (Y_f^(1/2) * P + 1)\]`

To find the partial elasticity at a specific point, you can substitute the given values for
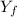`Y_f` and P. In this case, the elasticity is -1, indicating an inverse relationship between the price level and foreign demand. As our price level increases, foreign demand decreases proportionally.

In economic terms, a partial elasticity of -1 suggests that a 1% increase in our price level would lead to a 1% decrease in foreign demand for our exports, assuming foreign income remains constant. This implies a relatively elastic relationship between our price level and foreign demand.

Full Question:

The Foreign Demand For Our Exports X Depends On The Foreign Income
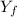`Y_f` And Our Price Level
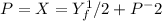`P = X = Y_f^1/2 + P^-2`. Find the partial elasticity of foreign demand for our exports with respect to our price level.

Answer 2

The following represents the partial elasticity of foreign demand for our exports relative to our price level::
`E = (-2/P^2) * (1/(Y^(^1^/^2^) + 1/P^2))`

Step-by-step explanation:

We can use the following formula to determine the partial elasticity of foreign demand for our exports relative to our price level:

E = (∂X/∂P) * (P/X)

Where:

• - E is the exports' partial elasticity of demand from overseas relative to our price level.
• - The partial derivative of foreign demand relative to the price level is denoted by - (∂X/∂P).
• - P is the price level.
• -Global demand for our exports is represented by X.

Now let's use this formula to solve the provided equation:

`X = Y^(1/2) + P^(^-^2^)`

To find (∂X/∂P), we need to differentiate the equation with respect to P:

(∂X/∂P) = 0 + (-2)P⁻³ = -2/P³

Now, we can substitute (∂X/∂P) and the given values into the elasticity formula:

`E = (-2/P^3) * (P/X)`

Since X = Y^(1/2) + P^(-2), we can rewrite X as:

`X = Y^(1/2) + P^(^-^2^) = Y^(1^/^2^) + 1/P^2`

Now, we can substitute X into the elasticity formula:

`E = (-2/P^3) * (P/(Y^(^1^/^2^) + 1/P^2))`

Simplifying further:

`E = (-2/P^2) * (1/(Y^(^1^/^2^) + 1/P^2))`

As a result, the following represents the partial elasticity of foreign demand for our exports relative to our price level:

`E = (-2/P^2) * (1/(Y^(^1^/^2^) + 1/P^2))`