Question

A warehouse worker is pushing a 90.0 kg crate with a hocizootal force of 291 N at a speed of V=0.860 m/s across the wareheuse floor. He encounters a reough horirantal sectlon of the floor that is 0.75 m long aed where the coefficent of kinetic friction betaeen the crate and floor is 0.355. (a) Determine the magnitude and direction of the net force acting on the crate while it is pushed over the rough section of the floor. magnitude Have you drawn a force diagram and identified all forces acting on the crate? N direction (b) Determine the net work done on the crate while it is pushed over the rough section of the floor. Can you write an expression for the net work done on the crate in terms of the net force acting on the crate? J (c) Find the speed of the crate when it reaches the end of the rough surface. Can you develop an expression for the final speed of the crate in terms of its initial speed and the net work done on it? m/s

Answer 1

The magnitude and direction of the net force acting on the crate can be determined by considering the forces involved, including gravity, normal force, and friction. The net work done on the crate can be calculated by multiplying the magnitude of the net force by the distance. The final speed of the crate can be found using the work-energy principle.

Step-by-step explanation:

To determine the magnitude and direction of the net force acting on the crate as it is pushed over the rough section of the floor, we need to consider all the forces acting on the crate. The forces include the force of gravity, the normal force, and the frictional force. The net force can be found by subtracting the frictional force from the applied force. The magnitude of the net force is 291 N - (0.355 * 90.0 kg * 9.8 m/s^2), and the direction of the net force is opposite to the direction of motion of the crate.

The net work done on the crate can be determined by multiplying the magnitude of the net force by the distance over which it is applied. In this case, the distance is 0.75 m. The expression for the net work done on the crate is W = F * d = (291 N - (0.355 * 90.0 kg * 9.8 m/s^2)) * 0.75 m.

The final speed of the crate can be found using the work-energy principle. The net work done on the crate is equal to the change in its kinetic energy. We can write an expression for the final speed of the crate in terms of its initial speed and the net work done on it. The expression is v_f^2 = v_i^2 + 2a_f * d, where v_f is the final speed, v_i is the initial speed, a_f is the acceleration, and d is the distance over which the net work is done. The net work done on the crate is divided by the mass of the crate to find the acceleration, and the initial speed is squared to find the final speed.

Answer 2

Part (a): Net force magnitude = 21.8 N, direction = opposite to the pushing force.

Part (b): Net work done = -16.35 J (negative due to work done against friction).

Part (c): Final speed of the crate = 0.803 m/s (slightly slower than the initial speed).

Part (a): Net Force on the Crate

Identify forces: Draw a force diagram showing the following forces acting on the crate:

Horizontal pushing force
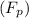`(F_p)`: 291 N, directed forward.

Friction force
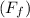`(F_f)`: Opposes the direction of motion, with magnitude
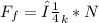`F_f = μ_k * N`, where
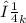`μ_k` is the coefficient of kinetic friction (0.355) and N is the normal force (equal to the weight of the crate, 90.0 kg * 9.81 m/s²).

Weight (W): 90.0 kg * 9.81 m/s², acting downward.

Calculate normal force: Since the floor is horizontal, the normal force is equal to the weight of the crate: N = W = 90.0 kg * 9.81 m/s² = 882.9 N.

Calculate friction force:
`F_f` =
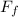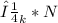`μ_k * N` = 0.355 * 882.9 N ≈ 312.8 N.

Net force: The net force is the sum of all forces acting on the crate. Since the pushing force and the friction force are in opposite directions, we have:

Net force (
`F_net`) =
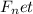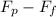`F_p - F_f` = 291 N - 312.8 N ≈ -21.8 N (Negative sign indicates a net force in the opposite direction of the pushing force).

Part (b): Net Work Done on the Crate

Net work definition: Work is the product of force and displacement in the direction of the force. Since the net force is acting against the direction of movement (0.75 m), the work done is negative:

Net work (
`W_net`) =
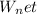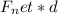`F_net * d` = (-21.8 N) * (0.75 m) ≈ -16.35 J.

Part (c): Final Speed of the Crate

Work-energy principle: The work done on the crate is equal to the change in its kinetic energy:

W_net =
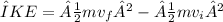`ΔKE = ½ mv_f² - ½ mv_i²` where m is the mass of the crate (90.0 kg),
`v_i` is the initial speed (0.860 m/s), and
`v_f` is the final speed (unknown).

Solve for
`v_f`: Rearrange the equation and solve for
`v_f:`

`v_f² = v_i² + (2 * W_net) / m`

`v_f² = 0.860² + (2 * (-16.35 J)) / 90.0 kg`

`v_f² ≈ 0.645 m²/s²`

`v_f ≈ 0.803 m/s`

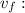
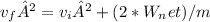
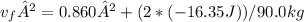
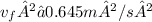
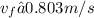
(Note that the final speed is lower than the initial speed due to the work done against friction).