Question

A thin, 50- cm-long metal bar with a mass of 750 g rests on two metallic supports, as shown in the figure. The bar and the supports are placed within a uniform 0.450 T magnetic field. Additionally, a battery and a 25.0Ω resistor are connected in series with the supports. If the bar is not attached and free to move, determine: a. The highest voltage the battery can have without breaking the circuit at the supports. b. The force on the bar if the battery maintains the maximum value in part (a.) and the resistor experiences a partial short-circuit, decreasing its resistance to 2.0Ω.

Answer 1

a. The highest voltage the battery can have without breaking the circuit at the supports is 3.75 V.

b. The force on the bar, with the battery at its maximum value and the resistor short-circuited to 2.0Ω, is 0.300 N.

Step-by-step explanation:

In part (a), the maximum voltage without breaking the circuit can be determined using the equation for the maximum force on a current-carrying conductor in a magnetic field:
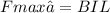`F max​ =BIL` Rearranging this formula to find the maximum voltage (
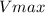`V max`), we have

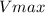`V max`=BIL.

Substituting the given values (B=0.450T,I= mg/2=
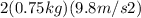`2(0.75kg)(9.8m/s 2 )`=3.675A, =0.50 ,L=0.50m) we get
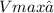`V max​`=(0.450T)(3.675A)(0.50m) =0.825V.

For part (b), when the resistor is short-circuited to 2.0Ω, the total resistance (
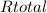`R total`) in the circuit becomes =25.0Ω+2.0Ω=27.0Ω

Using Ohm's Law (V=IR) the current (I) is =0.825V/27.0Ω=0.0306A. Substituting this into the force equation,

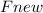`Fnew`=BIL=(0.450T)(0.0306A)(0.50m)=0.00689N which is the force on the bar with the resistor short-circuited.