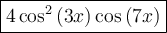Question

PLEASE HELP ME!!! 100 POINTS!!!

Express the following as a product using the sum-to-product formula:

cos(x)+2cos(7x)+cos(13x)

Answer 1

`4 \cos^2 \left(3x\right)\cos \left(7x\right)`

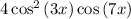
Explanation:

We have been given the following trigonometric sum:

`\cos(x)+2\cos(7x)+\cos(13x)`

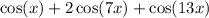
To express this sum as a product, we can use the cosine sum to product formula:

`\boxed{\begin{array}{c}\underline{\sf Sum\;to\;Product\;Formula}\\\\\cos A+ \cos B=2 \cos \left((A+B)/(2)\right) \cos \left((A-B)/(2)\right)\\\\\end{array}}`

Rewrite the trigonometric sum as:

`\cos(13x)+\cos(7x)+\cos(7x)+\cos(x)`

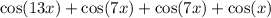
Apply the sum to product formula to the first two terms and the last two terms:

`2 \cos \left((13x+7x)/(2)\right) \cos \left((13x-7x)/(2)\right)}+2 \cos \left((7x+x)/(2)\right) \cos \left((7x-x)/(2)\right)`

`2 \cos \left((20x)/(2)\right) \cos \left((6x)/(2)\right)}+2 \cos \left((8x)/(2)\right) \cos \left((6x)/(2)\right)`

`2 \cos \left(10x\right) \cos \left(3x\right)+2 \cos \left(4x\right) \cos \left(3x\right)`

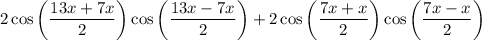
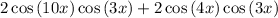
Factor out the common term 2cos(3x):

`2 \cos \left(3x\right)\left[\cos \left(10x\right) + \cos \left(4x\right) \right]`

Apply the sum to product formula again to the sum inside the parentheses, cos(10x) + cos(4x):

`2 \cos \left(3x\right)\left[2 \cos \left((10x+4x)/(2)\right) \cos \left((10x-4x)/(2)\right)\right]`

`2 \cos \left(3x\right)\left[2 \cos \left((14x)/(2)\right) \cos \left((6x)/(2)\right)\right]`

`2 \cos \left(3x\right)\left[2 \cos \left(7x\right) \cos \left(3x\right)\right]`

Remove the unnecessary parentheses:

`2 \cos \left(3x\right)2 \cos \left(7x\right) \cos \left(3x\right)`

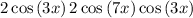
Multiply the numbers:

`4 \cos \left(3x\right)\cos \left(7x\right) \cos \left(3x\right)`

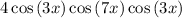
Rewrite cos(3x)cos(3x) as cos²(3x):

`4 \cos^2 \left(3x\right)\cos \left(7x\right)`

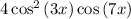
Therefore, the given trigonometric sum expressed as a product is:

`\large\boxed{4 \cos^2 \left(3x\right)\cos \left(7x\right)}`