Question

An L−C circuit containing an 80.0-mH inductor and a 1.25−nF capacitor oscillates with a maximum current of 0.75 A. Calculate: (a) the maximum charge on the capacitor and (b) the oscillation frequency of the circuit. (c) Assuming the capacitor had its maximum charge at time calculate the energy stored in the inductor after 2.50 ms of oscillation.

Answer 1

(a) The maximum charge on the capacitor is Q_max = 1.5 ×
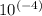`10^((-4))` C.

(b) The oscillation frequency of the circuit is f = 159 Hz.

(c) The energy stored in the inductor after 2.50 ms of oscillation is 3.75 ×
`10^((-5))` J.

Step-by-step explanation:

In part (a), to find the maximum charge on the capacitor
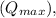`(Q_(max) ),` we use the formula
`(Q_(max) )` = (1/2) * C *
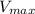`V_(max)`, where C is the capacitance and
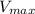`V_(max)` is the maximum voltage across the capacitor. Using the given values of the capacitor (1.25 nF) and the maximum current (0.75 A), we can determine the maximum voltage and then calculate the maximum charge.

For part (b), the oscillation frequency (f) of the L-C circuit can be found using the formula f = 1 / (2π *
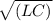`√((LC))`), where L is the inductance and C is the capacitance. Plugging in the provided values for the inductor (80.0 mH) and capacitor (1.25 nF), we can calculate the oscillation frequency.

In part (c), the energy stored in the inductor (W) after a given time can be found using the formula W = (1/2) * L *
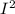`I^2`, where L is the inductance and I is the current. With the given time (2.50 ms) and the maximum current (0.75 A), we can determine the energy stored in the inductor during the specified time of oscillation.