Question

Consider the system of two blocks and a spring shown in (Figure 1). The horizontal surface is frictionless, but there is static friction between the two blocks. The spring has force constant k=250 N/m. The What is the period of the motion of the two blocks when d is small enough to have no slipping? masses of the two blocks are m=0.500 kg and M=9.00 kg. You Express your answer with the appropriate units. set the blocks into motion by releasing block M with the spring stretched a distance d from equilibrium. You start with small values of d, and then repeat with successively larger values. For small values of d, the blocks move together in SHM. But for larger values of d the top block slips relative to the bottom block when the bottom block is released. Figure Part B The largest value d can have and there be no slipping is 8.8 cm. What is the coefficient of static friction μ

s
​
between the surfaces of the two blocks? Express your answer to two significant figures.

Answer 1

The period of motion of the two blocks when d is small enough to have no slipping is approximately 1.225 s and the coefficient of static friction μ between the surfaces of the two blocks is 0.47 (approximately).

The period of the motion for a mass-spring system can be calculated using the formula:

`\[ T = 2\pi\sqrt{(m)/(k)} \]`

However, in the case of two blocks connected by a spring with static friction, the system will have two normal modes of oscillation. The general expression for the period of such a system is given by:

`\[ T = 2\pi\sqrt{(m)/(k)} \sqrt{(m+M)/(m)} \]`

Substituting the given values:

`\[ T = 2\pi\sqrt{\frac{0.500 \, \text{kg}}{250 \, \text{N/m}}} \sqrt{\frac{0.500 \, \text{kg} + 9.00 \, \text{kg}}{0.500 \, \text{kg}}} \]` =
`2\pi` (0.045)(4.36) = 1.225 s (approximately).

To find the coefficient of static friction between the surfaces of the two blocks,

Given:

The force constant of the spring, k = 250 N/m.

d = 8.8 cm = 0.088 m

The maximum force of static friction can be calculated using the equation:

`F_(s (max)) = u_(s) * F_(N)`

where
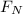`F_(N)` is the normal force between the blocks, and
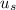`u_(s)` is the coefficient of static friction.

Since there is no slipping, the normal force is equal to the weight of the top block:

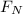`F_(N)` = m * g

where m is the mass of the top block and g is the acceleration due to gravity.

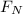`F_(N)` = 0.500 kg * 9.8 m
`s^(-2)`

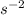
The spring constant can be related to the maximum force of static friction using the equation:

`F_(s (max)) = k * d`

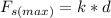
Combining the equations,

`u_(s) = (k d)/(m g)`

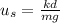
Substituting the given values into the equation, we get:

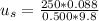`u_(s) = (250 * 0.088)/(0.500 * 9.8)` = 0.47

The coefficient of static friction is approximately 0.47 (rounded to two significant figures).

Answer 2

The coefficient of static friction μs can be calculated from the maximum spring displacement before slipping occurs and the spring constant, using the balance of forces between spring force and static friction.

Step-by-step explanation:

We are asked to find the coefficient of static friction μs between two blocks where block m is placed on top of block M and the system is connected to a spring. When the spring is stretched by a distance d and there is no slipping between the blocks, they move together in Simple Harmonic Motion (SHM). The maximum distance d where no slipping occurs provides the necessary information to calculate the coefficient of static friction using Newton's laws and the concept of SHM.

Using the maximum displacement without slipping and the spring constant k, we can calculate the spring force at this displacement, which is equal to the maximum static friction force. From this, using the fact that the static friction force is also equal to μs times the normal force (which is the weight of the top block), we can solve for μs.