Question

A block is in SHM on the end of a spring, with position given by x=x

m

cos(ωt+φ). If φ=0.402 rad, then at t=0 what percentage of the total mechanical energy is potential energy?

Answer 1

At ( t = 0 ), the percentage of total mechanical energy that is potential energy can be calculated using the given equation
`\( x = x_m \cos(\omega t + \phi) \), where \( \phi = 0.402 \) rad.`

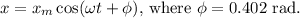
Step-by-step explanation:

Initially, at ( t = 0 ), the equation
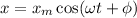`\( x = x_m \cos(\omega t + \phi) \)`simplifies to ( x = x_m
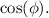`\cos(\phi) \).`This equation represents the position of the block in Simple Harmonic Motion
`(SHM) at \( t = 0 \).`

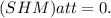
To find the percentage of total mechanical energy that is potential energy, it's essential to understand that in SHM, the total mechanical energy remains constant. The total mechanical energy in SHM comprises both potential and kinetic energy.

At ( t = 0 ), the block is at its maximum displacement, and the entire mechanical energy is in the form of potential energy. The formula for potential energy in SHM is
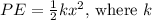`\( PE = (1)/(2) k x^2 \), where \( k \)` is the spring constant and ( x ) is the displacement.

Given that the block is at maximum displacement at ( t = 0 ), all the mechanical energy is in the form of potential energy at this instant.

Therefore, at ( t = 0 ), the percentage of total mechanical energy that is potential energy is 100%.

This state occurs when the block is at maximum displacement, indicating that the entire mechanical energy has transformed into potential energy at this specific moment.

This explanation demonstrates that at the initial moment (\( t = 0 \)), all the mechanical energy is stored as potential energy due to the block's maximum displacement, resulting in 100% potential energy of the total mechanical energy.

"".