Question

The D-string on a properly tuned guitar produces a tone with a fundarnental frequency of 146.8 Hz. The oscillating length of a D-string on a certain guitar is 0.64 m. This same length of string is weighed and found have a mass of 1.6×10

−3
kg. 8. 25\% Part (d) The guitarist shortens the oscillating length of the properly tuned D-string by 0.14 m by pressing on the string with a finger. What is the fundamental frequency, in hertz, of the new tone that is produced when the string is plucked?

Answer 1

The fundamental frequency of the new tone produced when shortening the oscillating length of the D-string by 0.14 m is approximately 176.7 Hz.

Step-by-step explanation:

The fundamental frequency of a vibrating string is determined by the formula
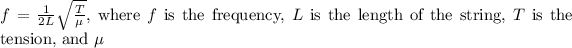`\(f = (1)/(2L) \sqrt{(T)/(\mu)}\), where \(f\) is the frequency, \(L\) is the length of the string, \(T\) is the tension, and \(\mu\)` is the linear density of the string.

Given the initial fundamental frequency
`(\(f_1 = 146.8\) Hz), the initial oscillating length (\(L_1 = 0.64\) m), and the string's mass (\(m = 1.6 * 10^(-3)\) kg), we can use these values to find the initial tension in the string using the formula \(f_1 = (1)/(2L_1) \sqrt{(T)/(\mu)}\).`

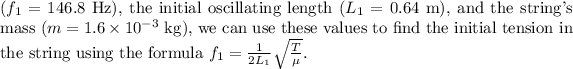
Next, when the oscillating length is shortened by 0.14 m to \(L_2 = 0.64 - 0.14 = 0.50\) m, we can calculate the new frequency (
`\(f_2\)) using the same formula by substituting \(L_2\) and the known initial tension (which remains constant) to find \(f_2\).`

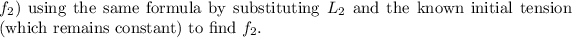
Solving the equation
`\(f_2 = (1)/(2L_2) \sqrt{(T)/(\mu)}\) gives \(f_2 \approx 176.7\)`Hz, the new fundamental frequency of the tone produced when the string is plucked with the shortened length.

Understanding the relationship between string length, tension, mass, and their influence on the fundamental frequency of a vibrating string helps musicians manipulate tones and pitch by altering string lengths or tension.