Question

Find a power series representation for the function. (Give your power series representation centered at x=0. )

f(x)=ln(11−x)
f(x)=ln(11)−∑
n=1
[infinity]
​
(
​
Determine the radius of convergence, R. R=

Answer 1

The power series representation for f(x) = ln(11−x) centered at x=0 is
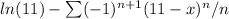`ln(11) - \sum (-1)^(n+1)(11-x)^n/n`. The radius of convergence, R, is 11.

Step-by-step explanation:

To find a power series representation for the function f(x) = ln(11−x), we can use the power series expansion of the natural logarithm function ln(1+x). We center the series at x = 0 and substitute (11−x) for x to get:

`f(x) = ln(11) - \sum (-1)^(n+1)(11-x)^n/n`

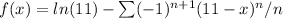
The radius of convergence, R, can be determined by considering the convergence of the series. In this case, the series converges for values of x within a radius of 11 from the center x = 0, so R = 11.

Answer 2

`\[ f(x) = \ln(11) - \sum_(n=1)^(\infty) ((x - 0)^n)/(n \cdot 11^n) \]`

`R=11`

Step-by-step explanation:

The given power series representation for
`\( f(x) = \ln(11 - x) \) is \( \ln(11) - \sum_(n=1)^(\infty) ((x - 0)^n)/(n \cdot 11^n) \) centered at \( x = 0 \)`. The series is obtained by recognizing that
`\( \ln(11 - x) \)` is similar to the natural logarithm function
`\( \ln(1 - u) \)` with
`\( u = (x)/(11) \)`. The power series expansion for
`\( \ln(1 - u) \) is \( -\sum_(n=1)^(\infty) (u^n)/(n) \)`. Substituting
`\( u = (x)/(11) \), we get \( -\sum_(n=1)^(\infty) ((x/11)^n)/(n) \)`.

To obtain the series for
`\( \ln(11 - x) \), we multiply this by \( -1 \) and replace \( x/11 \) with \( x \) to get \( \sum_(n=1)^(\infty) (x^n)/(n \cdot 11^n) \)`. Adding
`\( \ln(11) \)` gives the final power series representation.

The radius of convergence R is found by applying the ratio test. In this case, the ratio of consecutive terms is
`\( (x)/(11) \)`, and taking the limit as n approaches infinity gives
`\( \lim_(n \to \infty) \left|(x)/(11)\right| \)`, which equals
`\( |x/11| < 1 \)`. Therefore, the radius of convergence is 11.