The lower limit of integration a is
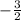 and the upper limit of integration b is
and the upper limit of integration b is
 . The side of the square cross-section s as a function of y is 4x or
. The side of the square cross-section s as a function of y is 4x or
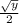 . The area function A(y) is 4y. The volume of the solid is 0.
. The area function A(y) is 4y. The volume of the solid is 0.
1. Finding the Limits of Integration:
The lower limit of integration a will be where the graphs intersect. Set
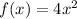 to find the intersection points:
to find the intersection points:
![\[9 = 4x^2\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/w2t8jvn1v5wquz9b384tkj5m7hmixijaid.png)
![\[x^2 = (9)/(4)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/cqsit2ala8gcd6qp7wemtywboawg01grix.png)
![\[x = \pm (3)/(2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/997p5gaq2cdnykcp36gemo2c7xex6hdmrr.png)
The upper limit of integration b will be the further x-value, so
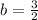 (since we're dealing with cross-sections perpendicular to the y-axis).
(since we're dealing with cross-sections perpendicular to the y-axis).
2. Finding the Side of the Square Cross-Section:
The side of the square cross-section is the difference in x-values for a given y-value (since these are squares perpendicular to the y-axis). It's 2x for the upper function (larger x-value) minus (-2x) for the lower function (smaller x-value):
![\[s(y) = 2x - (-2x) = 4x\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/4jzasz58sy2aqfxkl0p00wsbpbg1qwg6wf.png)
![\[x = \sqrt{(y)/(4)} = (√(y))/(2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/pe6k2yghjrsb9e5nn5qkk2vjqt9e959z9s.png)
3. Finding the Area Function A(y):
The area of the square cross-section is
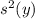 :
:
![\[A(y) = (4x)^2 = 16x^2 = 16 \cdot (y)/(4) = 4y\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/okn06ciy46koezxtpyu4resi7u1qkurojy.png)
4. Using the Volume Formula:
![\[V = \int_a^b A(y) \, dy = \int_{-(3)/(2)}^{(3)/(2)} 4y \, dy\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/gnpixg42zmcc26k05k1ljnlonp4rlwkahz.png)
Calculating the integral to find the volume.
![\[V = \int_{-(3)/(2)}^{(3)/(2)} 4y \, dy\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/d2pnnmid8ic4bsghst0l3aaxrekie7j4b7.png)
Integrating 4y with respect to y:
![\[V = 4 \int_{-(3)/(2)}^{(3)/(2)} y \, dy\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/u4azfm95yes1t8qzea1c1e6tyfjdae04vl.png)
The integral of y is
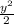 :
:
![\[V = 4 \left[(y^2)/(2)\right]_{-(3)/(2)}^{(3)/(2)}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hc9a458s63za0uuj9plc2pqcom52p05470.png)
![\[V = 4 \left((((3)/(2))^2)/(2) - ((-(3)/(2))^2)/(2)\right)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/32kxwxnklrawa6yj5l5qwb3vftqc55bjwq.png)
![\[V = 4 \left((9)/(8) - (9)/(8)\right)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6xuu7g1rb1a89hawddizkyjp4bux7wcxrq.png)
![\[V = 4 \cdot 0\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/xnaruq5fzj9i3bxf8r0u4bjbsga64n6o1m.png)
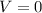
The volume of the solid is 0.
Question:
The base of a certain solid is the area bounded above by the graph of y = f(x) = 9 and below by the graph of y = 9(2) = 4x². Cross-sections perpendicular to the y-axis are squares.
Use the formula
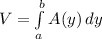
to find the volume of the formula.
Note: You can get full credit for this problem by just entering the final answer (to the last question) correctly. The initial questions are meant as hints towards the final answer and also allow you the opportunity to get partial credit.
The lower limit of integration is a = ___
The upper limit of integration is b = ____
The side s of the square cross-section is the following function of y ___
A(Y)= ___
Thus the volume of the solid is V = __