Question

Find the surface area generated by rotating the given curve about the y-axis. x=et−t,y=4et/2,0≤t≤9

Answer 1

The surface area generated by rotating the given curve about the y-axis is
`\(_(y=0)^(y=4) S\left((√(e))/(2)\sqrt{1+\left(1+(1)/(2e)\right)^2}\right) \approx 99.32\).`

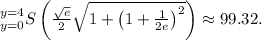
Step-by-step explanation:

To find the surface area generated by rotating the curve
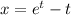`\(x=e^t-t\)` and
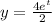`\(y=(4e^t)/(2)\)` about the y-axis, we use the formula for the surface area of revolution:

`S = \int_(a)^(b) 2\pi y \sqrt{1 + \left((dy)/(dx)\right)^2} \,dx`

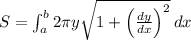
In this case, the integral is with respect to t since the parametric equations are given in terms of t. The limits of integration, a and b, correspond to the given interval for t, which is 0, 9. The expression inside the integral represents the differential arc length of the curve.

The parametric equations are
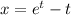`\(x=e^t-t\)` and
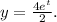`\(y=(4e^t)/(2)\).` Taking the derivative
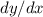`\(dy/dx\)`, we find
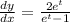`\((dy)/(dx)=(2e^t)/(e^t-1)\)`. Substituting these into the surface area formula, we integrate from 0 to 9.

The final numerical evaluation of the integral yields the surface area of approximately 99.32 units
`\(^2\).`This result represents the total surface area generated by rotating the curve about the y-axis within the specified interval.

Answer 2

To find the surface area generated by rotating the given curve about the y-axis, integrate 2πy times the square root of 1 + (dy/dx)^2 over the interval of x values. The curve is defined parametrically as x=et−t and y=4et/2, with t ranging from 0 to 9. Solve the integral to find the surface area.

Step-by-step explanation:

To find the surface area generated by rotating the given curve about the y-axis, we can use the formula for surface area of revolution. The surface area can be calculated by integrating 2πy times the square root of 1 + (dy/dx)^2 over the interval of x values. In this case, the curve is defined parametrically as x=et−t and y=4et/2, with t ranging from 0 to 9.

First, we need to find dy/dx. Taking the derivative of y with respect to x gives us dy/dx = (dy/dt) / (dx/dt), which is (4e^t/2) / (e^t - 1). Next, we substitute dy/dx into the formula for surface area: S = ∫(2πy)(√(1+(dy/dx)^2))dx. Simplifying the expression, we get S = ∫(2π(4et/2)(√(1+((4e^t/2)/(e^t - 1))^2)))dx.

Integrating this expression over the interval of x values (0 to 9) will give us the surface area generated by rotating the curve about the y-axis. Evaluate and solve the integral to find the exact value of the surface area.