Question

The smoothie chain makes multiple $0.15 increases to the average prices of their smoothies. The table shows the average profit of the chain compared to the number of price increases. The data models a quadratic function.

Use the data in the table to answer questions 3-5.
3. Use technology or hand calculations to determine the equation for the quadratic function modeled by the data in the table. Show an image of your final answer. (10 points)
4. Using the equation from question 3, determine the maximum profit. (5 points)
5. Using the equation from question 3, determine how many price increases will cause the smoothie chain to have zero profit. (7 points)

Answer 1

`\textsf{3)} \quad y=-0.01356x^2+3.74276x+117.91363`

`\textsf{4)} \quad 376\; \sf million`

`\textsf{5)} \quad 305 \sf\; price\;increases`

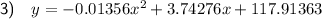
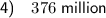
Explanation:

Question 3

Enter the (x, y) data from the given table into a suitable graphing calculator to create a quadratic equation that models the data in the table. (See attachment 1).

The quadratic equation is

`\large\text{$y=-0.01356x^2+3.74276x+117.91363$}`

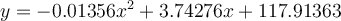
where each coefficient is rounded to 5 decimal places.

`\hrulefill`

Question 4

The maximum profit is the y-value of the vertex of the equation from question 3.

The formula to calculate the x-value of the vertex of a quadratic in the form ax² + bx + c is x = - b/2a. Therefore:

`x_(\sf vertex)=(-3.74276)/(2(-0.01356))=138.007374...`

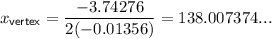
To find the y-value of the vertex, and hence the maximum profit (according to the equation from question 3), substitute the found x-value into the equation and solve for y:

`y=-0.01356(138.007374...)^2+3.74276(138.007374...)+117.91363`

`y=376.177870...`

`y=376\; \sf (nearest\;million)`

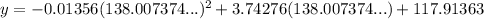
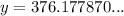
Therefore, the maximum profit (according to the equation from question 3) is 376 million.

Note: If we use the graphing calculator to find the vertex of the quadratic equation, y = 376.09101, which is 376 to the nearest million.

`\hrulefill`

Question 5

The number of price increases that will cause the smoothie chain to have zero profit is the value of x when y = 0.

To calculate this, set the equation from question 3 to zero and solve for x using the quadratic formula.

`\boxed{\begin{minipage}{4 cm}\underline{Quadratic Formula}\\\\$x=(-b \pm √(b^2-4ac))/(2a)$\\\\when $ax^2+bx+c=0$ \\\end{minipage}}`

The values of a, b and c are:

• a = -0.01356
• b = 3.74276
• c = 117.91363

Therefore:

`x=(-(3.74276) \pm √((3.74276)^2-4(-0.01356)(117.91363)))/(2(-0.01356))`

`x=(-3.74276 \pm √(20.4038877...))/(-0.02712)`

`x=(-3.74276 \pm4.51706627...)/(-0.02712)`

`x=304.565865...\\x= -28.5511162...`

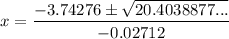
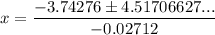
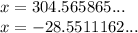
As the number of price increases is positive, we take the positive value of x only. Therefore, the number of price increases that will cause the smoothie chain to have zero profit is 305 (rounded to the nearest whole number).

Note: If we use the graphing calculator to find the points of intersection of the quadratic equation and the x-axis, x = 304 (rounded to the nearest whole number).