Question

19 In the diagram, 4 congruent right-angled triangles are arranged on each side of the square PQRS.

If the area of PQRS is 144x2 cm², calculate the perimeter of the whole diagram.
​

Answer 1

The perimeter is 72x cm

Explanation:

To calculate the perimeter, we need to find the hypotenuse of the triangles (same since they are congruent) and we are given the length of the side that will be used in the perimeter calculation i.e. 5x in the figure

Now, we can use the length of the square as the other side of the triangles and use that to calculate the hypotenuse.

Since the area of the square is 144x^2 cm^2,

we get,

144x^2 = l^2

Taking the square root,

`√(144x^2) =√(l^2) \\12x = l`

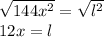
Hence l = 12x,

Now, using the pythagorean formula to find the hypotenuse,

c^2 = a^2 + b^2,

here, a = 5x and b = l = 12x so,

`c^2 = (5x)^2 + (12x)^2\\c^2 = 25x^2 + 144x^2\\c^2 =x^2(25+144)\\c^2 = 169x^2\\√(c^2) =√(169x^2) \\c=13x`

c = 13x,

We have foundthe hypotenuse,

Now, observing the figure, we see that the perimeter is the sum of 4 of the hypotenuses and 4 of the side length of 5x, so we get,

P = 4(5x) + 4(13x)

P = 20x + 52x

P =72x cm