Question

Two 4.0 kg masses are 3.0 m apart on a frictionless table. Each has 1.0 μC of charge.

PART A: What is the magnitude of the electric force on one of the masses? PART B: What is the initial acceleration of each mass if they are released and allowed to move?

Answer 1

Approximately
`1.0 * 10^(-3)\; {\rm N}`.

Approximately
`2.5 * 10^(-4)\; {\rm m\cdot s^(-2)}`.

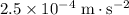Step-by-step explanation:

Assume that the volume of the two masses is negligible, such that each mass can each be considered as a point charge. Apply the following steps to solve this question:

• The magnitude of the electric force on the two masses can be found by applying Coulomb's Law.
• Assume that all other forces on the masses are balanced, such that the net force on each mass is equal to the electric force. Divide the net force on each object by mass to find the initial acceleration.

By Coulomb's Law, the electrostatic force on each mass would be:

`\displaystyle F = (k\, q_(1)\, q_(2))/(r^(2))`

Where:

• 
  `k \approx 8.9876 * 10^(9)\; {\rm N \cdot m^(2) \cdot C^(-2)}` is the Coulomb Constant,
• 
  `q_(1)` and
  `q_(2)` are the electrostatic charge on each object, and
• 
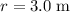  `r = 3.0\; {\rm m}` is the distance between the two charges.

It is given that
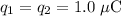`q_(1) = q_(2) = 1.0\; {\rm \mu C}`. Apply unit conversion and ensure that these values are measured in standard units (in coulombs, instead of in microcoulombs.)

`\begin{aligned}1.0\; {\rm \mu C} &= 1.0\; {\rm \mu C} * \frac{1\; {\rm C}}{10^(6)\; {\rm \mu C}} \\ &= 1.0* 10^(-6)\; {\rm C}\end{aligned}`.

Substitute these values into the Coulomb's Law expression and evaluate to find the electrostatic force between the two masses:

`\begin{aligned} F &= (k\, q_(1)\, q_(2))/(r^(2)) \\ &= ((8.9876* 10^(9))\, (1.0* 10^(-6))\, (1.0* 10^(-6)))/((3.0)^(2))\; {\rm N} \\ &\approx 9.9862 * 10^(-4)\; {\rm N}\end{aligned}`.

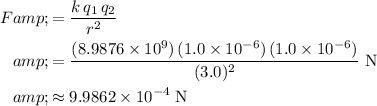Therefore, the magnitude of the electric force on each mass would be approximately
`1.0 * 10^(-3)\; {\rm N}` (rounded to two significant figures.)

Assume that all other forces on the two masses are balanced, such that the net force on each mass would be equal to the electrostatic force found above. Dividing the net force by mass would give the (initial) acceleration of the object:

`\begin{aligned}a &= \frac{(\text{net force})}{(\text{mass})} \\ &= \frac{(\text{electrostatic force})}{(\text{mass})}\\ &\approx \frac{9.9862 * 10^(-4)\; {\rm N}}{4.0\; {\rm kg}} \\ &\approx 2.5 * 10^(-4)\; {\rm m\cdot s^(-2)}\end{aligned}`.