Question

A company wants to design a box with four rectangular sides and a square top and bottom. a) Letting x denote the length of one of the sides of the bottom of the box, and letting y denote the height of the box, sketch a picture of the box, labeling the length, width, and height. The company wants to use exactly 81 cm

2
of material for the box. That is, the box's surface area will be equal to 81 cm
2
. Write an equation in terms of x and y representing this constraint, putting the variables on the left side. =cm
2
Solve for y to find y as a function of x. y= b) Using your work from part (a), write a formula for the volume of the box, V(x), as a function of x. Simplify as much as possible. V(x)= c) Use an online source to approximate the maximum value of V(x) on the interval [0,10]. What x value corresponds to this maximum value? What does this mean in the context of the problem? A. This is the length of the side of the box that produces the maximum volume of a box with a surface area of 81 cm
2
. B. This is the area of the base of the box that produces the maximum volume of a box with a surface area of 81 cm
2
. C. This is the maximum volume of a box with a surface area of 81 cm
2
.

Answer 1

Final answer:

A company wants to design a box with specific dimensions and a surface area of 81 cm². The equation in terms of x and y representing this constraint is 2x² + 4xy = 81 cm². The volume formula for the box is V(x) = x² * (81 - 2x²) / (4x), and the maximum volume can be found using an online source or a graphing calculator.

Step-by-step explanation:

a) Sketch:

To represent the box, draw a square on top and bottom, and four rectangles for the sides. Label the length of one side of the bottom as x, and the height of the box as y.

Equation:

The surface area of the box is made up of the areas of the six sides. The area of the top and bottom squares is 2x², and the area of the four rectangles is 4xy. So the equation is: 2x² + 4xy = 81 cm².

Solve for y:

Rearrange the equation to solve for y: y = (81 - 2x²) / (4x).

b) Volume Formula:

The volume of the box is the product of its base area and height. The base area is x², so the volume formula is: V(x) = x² * y = x² * (81 - 2x²) / (4x).

c) Maximum Volume:

Using an online source or a graphing calculator, find the maximum value of V(x) on the interval [0,10]. The x value that corresponds to this maximum value is the length of the side of the box that produces the maximum volume of a box with a surface area of 81 cm².

Answer 2

a) The equation representing the surface area constraint is
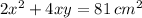`\(2x^2 + 4xy = 81\, cm^2\)`. Solving for y in terms of x,
`\(y = (81 - 2x^2)/(4x)\`.

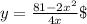b) The formula for the volume of the box,
`\(V(x)\)`, is
`\(V(x) = x^2 \cdot (81 - 2x^2)/(4x)\)`.

c) The maximum volume of the box with a surface area of 81 cm^2 occurs at x ≈ 3.80 cm. This corresponds to A. This is the length of the side of the box that produces the maximum volume of a box with a surface area of 81 cm^2.

Step-by-step explanation:

To represent the surface area constraint, we first establish the equation. Given that the box has four rectangular sides and square top/bottom, the surface area equation becomes
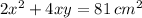`\(2x^2 + 4xy = 81\, cm^2\)` (where x represents the side length of the square base, and y is the height of the box). Solving for y in terms of x gives
`\(y = (81 - 2x^2)/(4x)\)`.

Next, to find the volume V(x) as a function of x, the formula for volume
`\(V\) is \(V(x) = x^2 \cdot y\)`. Substituting the expression for y in terms of x into the volume formula gives
`\(V(x) = x^2 \cdot (81 - 2x^2)/(4x)\)`. Simplifying this equation provides the volume of the box in terms of the side length x.

Using an online tool to determine the maximum value of V(x) on the interval [0,10], it approximates the maximum volume occurs at x ≈ 3.80 cm. This means that this x-value corresponds to the length of the side of the box that maximizes the volume given the surface area constraint of 81 cm². Hence, the answer aligns with option A, indicating the side length that generates the maximum volume for the specified surface area.