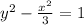Explanation:
Equation of an hyperbola is either
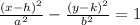
Or
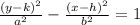
The variable
(h,k) is the center of hyperbola
Since (0,0) is the center, we can just use this equation
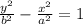
In this case, notice the focus and center both lie on the y axis, that means we have a vertical hyperbola so we will use the second equation for the hyperbola
The variable a is the semi major axis.(transverse axis)
The variable b is the semi minor axis (conjugate axis)
The vertex of a vertical hyperbola can be described as
(h,k+a),
The vertex is (0,0+1), so a is 1.
The focus of a vertical hyperbola can be described as
(h,k+c)
Where
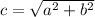
We know that c is 2 and a is 1.
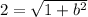
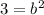
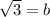
So our equation is