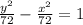Foci at $ (0,-12) $ and $ (0,12) $; asymptote the line $ y=-x $

Question

asked Aug 26, 2024 212k views

1 Answer

Manuel Pap · Answer 1 · 2024-08-31T22:00:42+0000

Explanation:

Since the foci lies on the y axis, we will be using the vertical ellipse equation

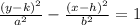
$\frac{(y - k) {}^(2) }{ {a}^(2) } - \frac{(x - h) {}^(2) }{ {b}^(2) } = 1$

Notice that the foci is (0,-12) and (0,12), that means the center,(h,k) is (0,0)

So our new equation is

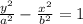
$\frac{ {y}^(2) }{ {a}^(2) } - \frac{ {x}^(2) }{ {b}^(2) } = 1$

To find the asymptotes of the hyperbola , set it equal to

$\frac{ {y}^(2) }{ {a}^(2) } - \frac{ {x}^(2) }{ {b}^(2) } = 0$

Difference of Squares

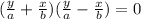
Set both equations equal to zero , and solve for y

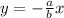
or

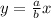
Notice that one of our asymptotes slope is -1. That means a and b are both the same number, so we can represent them as a singular variable,u,.

The equation of a focus is

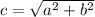
$c = \sqrt{ {a}^(2) + {b}^(2) }$

Here, c is 12

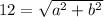
$12 = \sqrt{ {a}^(2) + {b}^(2) }$

Remember that both a and b are equal to each other so let u =a, and u=b

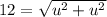
$12 = \sqrt{ {u}^(2) + {u}^(2) }$

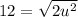
$12 = \sqrt{2 {u}^(2) }$

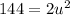
$144 = 2 {u}^(2)$

$72 = {u}^(2)$

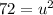
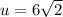
So our equation is

$\frac{ {y}^(2) }{72} - \frac{ {x}^(2) }{72} = 1$