Question

Find an equation for the hyperbola described. Graph the equation by hand. Foci at (−26,0) and (26,0); vertex at (24,0) An equation of the hyperbola is =1 (Use integer or fraction for any number in the expression.)

Answer 1

The equation of the hyperbola is
`\((x-24)^2/625 - y^2/576 = 1\)`.

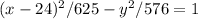Step-by-step explanation:

To find the equation of the hyperbola, we can use the standard form for the equation of a hyperbola centered at (h, k):

`\[\frac{{(x - h)^2}}{{a^2}} - \frac{{(y - k)^2}}{{b^2}} = 1\]`

In this case, the foci are given as (-26, 0) and (26, 0), and the vertex is (24, 0). The distance from the vertex to each focus is the value of
`c` in the standard form. The value of
`a` is the distance from the vertex to the corresponding end of the transverse axis, and
`b` is the distance from the vertex to the corresponding end of the conjugate axis.

The distance between the foci is
`\(2c = 2 * 26 = 52\)`, so c = 26. Since the hyperbola is centered at (h, k) = (24, 0), the value of
`a` is the distance from the center to the vertex, which is a = 24 - 24 = 0. The value of
`b` can be found using the Pythagorean theorem:

`\(a^2 + b^2 = c^2\)`.

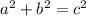Therefore,

`\(b^2 = 26^2 - 0^2 = 676\)`.

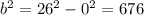Substituting these values into the standard form equation, we get:

`\[\frac{{(x - 24)^2}}{{0^2}} - \frac{{y^2}}{{676}} = 1\]`

Simplifying, we obtain:

`\[\frac{{(x - 24)^2}}{{625}} - \frac{{y^2}}{{676}} = 1\]`

Therefore, the equation of the hyperbola is
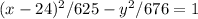`\((x-24)^2/625 - y^2/676 = 1\)`.