Question

Find the maximum area of a triangle formed in the first quadrant by the \( x \)-axis, \( y \)-axis and a tangent line to the graph of \( f=(x+10)^{-2} \). Area =

Answer 1

The maximum area of a triangle formed in the first quadrant by the
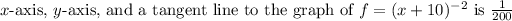`\( x \)-axis, \( y \)-axis, and a tangent line to the graph of \( f=(x+10)^(-2) \) is \( (1)/(200) \)` square units.

Step-by-step explanation:

To find the maximum area of the triangle formed by the given function, we need to consider the tangent line that intersects the graph in the first quadrant. The function
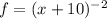`\( f=(x+10)^(-2) \)` represents a hyperbola, and its tangent line in the first quadrant will be parallel to the y-axis.

Let's denote the point of tangency as
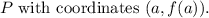`\( P \) with coordinates \((a, f(a))\).`The slope of the tangent line is given by the derivative of the function evaluated at
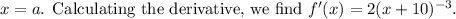`\( x=a \). Calculating the derivative, we find \( f'(x) = 2(x+10)^(-3) \).` Setting
`\( f'(a) \) equal to zero gives \( a=-10 \).`

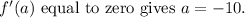
Now, the base of the triangle is twice the x-coordinate of the point of tangency, so
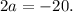`\( 2a=-20 \).` The height of the triangle is the y-coordinate of the point of tangency, which is
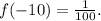`\( f(-10) = (1)/(100) \).` Therefore, the area
`\( A \)` is given by
`\( A = (1)/(2) * \text{base} * \text{height} = (1)/(2) * (-20) * (1)/(100) = (1)/(200) \) square units`.

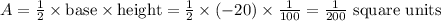Thus, the maximum area of the triangle is
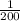`\( (1)/(200) \)`square units.