The correct option c.
To determine the intervals where the given function
 is concave up or concave down, we need to find the second derivative and analyze its sign.
is concave up or concave down, we need to find the second derivative and analyze its sign.
1. Find the first derivative
 :
:
![\[ F'(x) = 4x^3 - 9x^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/cozumr1dantmd0quq2u94v9yt13ngtrw32.png)
2. Find the second derivative
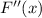 :
:
![\[ F''(x) = 12x^2 - 18x \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/mhvevxwdrbqscmzmmo9hfrjmxszxjuq3ri.png)
Now, set
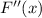 equal to zero and solve for x:
equal to zero and solve for x:
![\[ 12x^2 - 18x = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/789tbwx2tnx9bxaeq58lr2vc9lkuh7euw4.png)
Factor out
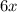 :
:
![\[ 6x(2x - 3) = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/pfccokvpi46w69h3bdzvjrs5fpsgg6eu33.png)
This gives
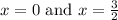 as critical points.
as critical points.
Now, test the intervals created by these critical points using the second derivative test:
- For
 , choose
, choose
 (test point).
(test point).
![\[ F''(-1) = 12(-1)^2 - 18(-1) = 30 > 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/3zapxt9zbrxirth0qmrj8z74vav4sm118s.png)
The function is concave up on
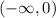 .
.
- For
 , choose
, choose
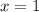 (test point).
(test point).
![\[ F''(1) = 12(1)^2 - 18(1) = -6 < 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/he31kllaivp8q730pveh3fxwyo6sro3wvt.png)
The function is concave down on
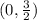 .
.
- For
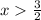 , choose
, choose
 (test point).
(test point).
![\[ F''(2) = 12(2)^2 - 18(2) = 12 > 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hnvhb5vghcbvulj05a13sj9ginuqi1ew4z.png)
The function is concave up on
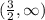 .
.
Therefore:
- The function is concave up on
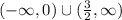
- The function is concave down on
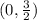 .
.
In interval notation:
A. The function is concave down on
![(0, (3)/(2)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/374kmrzhtdq7yll7m3yga69eiyxgk1pxb3.png)
B. The function is concave up on
![(-\infty, 0) \cup ((3)/(2), \infty) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nexzhd4wzi8ovyrtjeuzlz0585xkhwnjqo.png)
C. The function is concave up on
![(-\infty, 0) \cup ((3)/(2), \infty) \text{ and concave down on } (0, (3)/(2)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vjpuylu5z61qxzl9pkq3i8wsvlm356l0pl.png)