The general solution to the differential equation is:
y = e^(4x)((c1 + c2x)cos(x) + (c3 + c4x)sin(x))
Explanation of the solution:
-
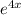 : This exponential term represents a fundamental solution to a homogeneous linear differential equation with constant coefficients. It indicates that the solution grows or decays exponentially as x changes.
: This exponential term represents a fundamental solution to a homogeneous linear differential equation with constant coefficients. It indicates that the solution grows or decays exponentially as x changes.
- (c1 + c2x)cos(x) + (c3 + c4x)sin(x): This part of the solution involves a combination of sine and cosine functions, which are typical for second-order homogeneous linear differential equations. The constants c1, c2, c3, and c4 represent arbitrary constants that can be determined based on initial or boundary conditions.
Key points:
- The differential equation is fourth-order, meaning it involves the fourth derivative of the unknown function y.
- It is homogeneous, meaning the right-hand side of the equation is zero (no external forcing terms).
- It has constant coefficients, meaning the coefficients of the derivatives of y are fixed numbers.
If you have specific initial or boundary conditions, I can help you determine the values of the constants c1, c2, c3, and c4 to obtain a particular solution that satisfies those conditions.
To find the derivatives of the given function
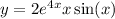 , we'll use the product rule, chain rule, and basic derivative rules. Let's go step by step:
, we'll use the product rule, chain rule, and basic derivative rules. Let's go step by step:
Given function:
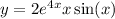
1. First Derivative
 :
:
Apply the product rule
 where
where
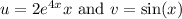 .
.
![\[ (dy)/(dx) = (2e^(4x) \cdot 1 \cdot x + 2e^(4x) \cdot 1 \cdot \sin(x)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/gvcukr5rlhj3n3n1x9ela94o2i97k62lay.png)
![\[ (dy)/(dx) = 2e^(4x)(x + \sin(x)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/blhg2km0l1kp1eicqsr6ylf7gwu5xef9ew.png)
2. Second Derivative
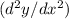 :
:
Apply the product rule again on the first derivative.
![\[ (d^2y)/(dx^2) = 2e^(4x)(1 + 4x) + 2e^(4x)(x + \sin(x)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rx6x7m40yi3lfut5f8wu8h8xy6rf21lnth.png)
Simplify further if needed.
3. Third Derivative
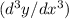 :
:
Apply the product rule to the second derivative.
![\[ (d^3y)/(dx^3) = 2e^(4x)(4 + 16x) + 2e^(4x)(1 + 4x) + 2e^(4x)(x + \sin(x)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/tgcnkp5qb9z6nl76plp8wxy6tvgbqtrspi.png)
4. Fourth Derivative
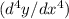 :
:
Apply the product rule to the third derivative.
![\[ (d^4y)/(dx^4) = 2e^(4x)(16 + 16) + 2e^(4x)(4 + 16x) + 2e^(4x)(1 + 4x) + 2e^(4x)(x + \sin(x)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ja68euwlp3vawqnn03uekjgz59afdvrdsk.png)
Simplify further if needed.
Keep in mind that these expressions can be simplified further, and you may use symbolic calculators or software to obtain more concise forms of the derivatives.
Complete the question:
Suppose that a fourth order differential equation has a solution
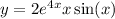 . Find such a differential equation, assuming it is homogeneous.
. Find such a differential equation, assuming it is homogeneous.