Final Answer:
The definite integral ∫_{0}¹⁰ f(x)dx is equal to 60.The signed area under the curve of the function f(x) = {
3x − 15 (0 ≤ x < 5)
15 − 3x (5 ≤ x ≤ 10)
} from 0 to 10 can be visualized as the combination of two regions. The first region, corresponding to the interval [0,5), represents the area above the x-axis minus the area below the x-axis, resulting in a net positive signed area.
Step-by-step explanation:
The given function f(x) is defined differently for two intervals: [0,5) and [5,10]. To evaluate the definite integral ∫_{0}^{10} f(x)dx, we need to split the integral into two parts corresponding to these intervals and then calculate each part separately.
For the interval [0,5), the function is 3x - 15. The definite integral for this interval is ∫_{0}^{5} (3x - 15)dx. To find the antiderivative, we integrate each term separately:
 15 dx. Evaluating these integrals, we get
15 dx. Evaluating these integrals, we get
![[(3/2)x^2]_(0)^(5) - [15x]_(0)^(5),](https://img.qammunity.org/2024/formulas/mathematics/high-school/6lppkvk7imxdazysq2iahsa6khooa4ldya.png) which simplifies to (3/2) * 5^2 - 15 * 5 - (0 - 0) = 37.5.
which simplifies to (3/2) * 5^2 - 15 * 5 - (0 - 0) = 37.5.
For the interval [5,10], the function is 15 - 3x. The definite integral for this interval is ∫_{5}^{10} (15 - 3x)dx. Integrating each term separately, we get
![[15x - (3/2)x^2]_(5)^(10),](https://img.qammunity.org/2024/formulas/mathematics/high-school/iirlpollwx0tp6l6tz302lkdsye5icze10.png) which simplifies to 150 - (75/2) - (75 - 37.5) = 22.5.
which simplifies to 150 - (75/2) - (75 - 37.5) = 22.5.
Adding these two results together, we get the final answer: 37.5 + 22.5 = 60. Therefore, ∫_{0}
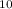 f(x)dx = 60, representing the signed area under the curve.
f(x)dx = 60, representing the signed area under the curve.