Question

Let X be a random variable with a variance of 2.0, and let Y be a random variable with a variance of 9.0. Let the covariance of X and Y be equal to half of the variance of X. Find the variance of 7X+Y.

Answer 1

To find the variance of 7X + Y, we can use the properties of variance and covariance.

First, let's Indicate the givens

• variance of X as Var(X) = 2.0
• variance of Y as Var(Y) = 9.0
• covariance of X and Y as Cov(X, Y) = 0.5 × Var(X).

Now, we need to find the variance of 7X + Y, signify as Var(7X + Y)

`\tt \tiny\: Var(aX + bY) = a^2 * Var(X) + {b}^(2) * Var(Y) + 2ab * Cov(X, Y)`

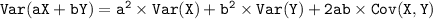
In this case, a = 7 and b = 1 , then let's substitute the given values

So,

`\tt \tiny \: Var(7X + Y) = (7^2) * Var(X) + (1^2)\\ \tt \tiny\: * Var(Y) + 2 * (7) * (1) * Cov(X, Y)`

`\tt \tiny \: Var(7X + Y) = 49 * Var(X) + Var(Y) + 14 * Cov(X, Y)`

`\tt \tiny \: Var(7X + Y) = 49 * 2.0 + 9.0 +14 * (0.5 * Var(X))`

`\tt \tiny \:Var(7X + Y)= 98.0 + 9.0 + 14.0`

`\boxed{ \tt \: Var(7X + Y) = \green{ 121.0}}`

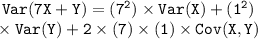
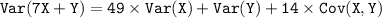
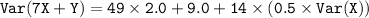
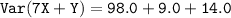
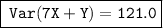
Therefore, the variance of 7X + Y is 121.0.