Question

A stunt car needs to get over a 22 m long jump. The car can travel at 72 m/s. If the car is launched straight forward off a ledge, what needs to be the height of the ledge so that the car will make a leap successfully?

Answer 1

0.46 m.

Step-by-step explanation:

Given:

Range(R) : 22 m

Since it is a the horizontal component:

initial velocity(u)= 72 m/s

Height(h)=?

Since

When range, initial and initial velocity are given, we can use Horizontal Range formula:

That is:

`\boxed{\tt R=u\sqrt{(2h)/(g)}}`

where,

R= Range

u = initail velocity

h=height

g= acceleration due to gravity which 9.8 m/s^2

Now,

Substituting value

`\tt 22 = 72\sqrt{(2h)/(9.8)}`

solving for h

dividing both side by 72.

`\tt (22)/(72)=\sqrt{(2h)/(9.8)}`

squaring both side

`\tt (0.306)^2=(2h)/(9.8)`

multiplying both side by
`\tt (9.8)/(2)`

`\tt 0.093*(9.8)/(2)=h`

`\tt h= 0.46 m`

Therefore, the height of the ledge needs to be approximately 0.46 m.

Answer 2

0.46 m (2 d.p.)

Step-by-step explanation:

A projectile is an object which has been projected through the air.

To solve problems involving projectile motion using the constant acceleration equations (SUVAT), we need to make certain assumptions:

• The projectile is moving only under the influence of gravity.
• The projectile is a particle.
• The projectile moves in a two-dimensional vertical plane.

As we have not been given any information about other forces (such as wind resistance), the dimensions of the car, or if it is swerving from side to side, we can model the car as a particle, assume it is moving only under the influence of gravity, and moving in a two-dimensional plane. Therefore, we can use the constant acceleration equations to find the height of the ledge.

Constant Acceleration Equations (SUVAT)

`\boxed{\begin{array}{c}\begin{aligned}v&=u+at\\\\s&=ut+(1)/(2)at^2\\\\ s&=\left((u+v)/(2)\right)t\\\\v^2&=u^2+2as\\\\s&=vt-(1)/(2)at^2\end{aligned}\end{array}} \quad \boxed{\begin{minipage}{4.6 cm}$s$ = displacement in m\\\\$u$ = initial velocity in m/s\\\\$v$ = final velocity in m/s\\\\$a$ = acceleration in m/s$^(2)$\\\\$t$ = time in s (seconds)\end{minipage}}`

When approaching projectile questions, we need to consider the horizontal and vertical motion of the projectile separately.

We are told that the car is launched straight forward off a ledge, so the projectile is fired horizontally. Therefore:

• The horizontal component of its initial velocity is 72 m/s.
• The vertical component of its initial velocity is zero.

Begin by calculating the time it takes for the car to travel 22 meters horizontally by resolving horizontally. (Note, there is no acceleration horizontally).

Given values:

• s = 22 m
• u = 72 m/s
• a = 0 m/s²

`\begin{aligned}\textsf{Using}\;\;s&=ut+(1)/(2)at^2\\\\\implies 22&=72t+(1)/(2)(0)t^2\\\\22&=72t\\\\t&=(22)/(72)\\\\t&=(11)/(36)\; \sf s\end{aligned}`

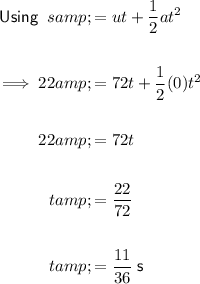
Therefore, the time it takes for the car to travel a horizontal distance of 22 m is 11/36 seconds.

Now we have calculated the time, we can calculate the vertical height of the ledge by resolving vertically.

As the projectile is fired horizontally, the vertical component of its initial velocity is zero, so u = 0 m/s.

Acceleration due to gravity is a = 9.8 m/s².

Resolving vertically, taking ↓ as positive, we have the values:

• u = 0 m/s
• a = 9.8 m/s²
• t = 11/36 s

`\begin{aligned}\textsf{Using}\;\;s&=ut+(1)/(2)at^2\\\\\implies s&=(0)\left((11)/(36)\right)+(1)/(2)(9.8)\left((11)/(36)\right)^2\\\\s&=0.457484567...\\\\s&=0.46\; \sf m\;(2\;d.p.)\end{aligned}`

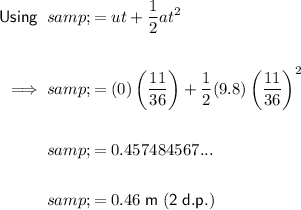
Therefore, the height of the ledge needs to be approximately 0.46 m (2 d.p.) for the car to successfully make a leap over a 22 m long jump.