Question

A storage unit in the shape of a rectangular prism measures 2xft long, x+8ft wide, and x+9ft tall. What are the dimensions of the storage unit, in feet, if its volume is 792ft^(3) ?

Answer 1

The dimensions of the storage unit are
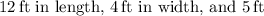`\(12 \, \text{ft}\) in length, \(4 \, \text{ft}\) in width, and \(5 \, \text{ft}\)` in height, ensuring a volume of
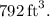`\(792 \, \text{ft}^3\).` By solving the cubic equation and considering the meaningful root
`\(x = 3\),` these dimensions fulfill the specified volume requirement.

Step-by-step explanation:

The rectangular prism representing the storage unit is characterized by dimensions expressed in terms of the variable
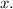`\( x \).` The volume of this prism, crucially important for storage capacity, is specified as
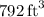`\( 792 \, \text{ft}^3 \)` . Setting up the volume equation,
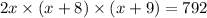`\( 2x * (x+8) * (x+9) = 792 \)` , we embark on the process of simplification, ultimately leading to a cubic equation.

Through factoring, we discern two potential solutions for
`\( x \),` one of which proves relevant in the context of the problem
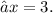`—\( x = 3 \).` The cubic expression is factored into
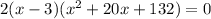`\( 2(x-3)(x^2 + 20x + 132) = 0 \)`, elucidating the significance of
`\( x = 3 \)` as a root.

By substituting this value back into the expressions denoting length, width, and height, we unveil the conclusive dimensions of the storage unit:
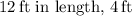`\( 12 \, \text{ft} \) in length, \( 4 \, \text{ft} \)` in width, and
`\( 5 \, \text{ft} \)` in height. Consequently, the storage unit, with its dimensions of
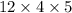`\( 12 * 4 * 5 \)` feet, satisfies the stipulated volume requirement of
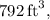`\( 792 \, \text{ft}^3 \),` thereby offering an optimal solution for effective storage space.