Question

A 10cm×10cm×10cm wood block with a density of 730 kg/m3 floats in water.

What is the distance from the top of the block to the water if the water is fresh?

Answer 1

The distance from the top of the 10cm × 10cm × 10cm wood block to the water, when it is floating in fresh water with a density of 730 kg/m³, is 5.5 cm.

Step-by-step explanation:

When an object floats in a fluid, the buoyant force acting on it is equal to the weight of the fluid it displaces. In this case, the buoyant force exerted by the water on the block is equal to the weight of the block. The buoyant force (B) can be calculated using the formula B = ρ * V * g, where ρ is the density of the fluid (fresh water in this case), V is the volume of the fluid displaced by the object, and g is the acceleration due to gravity.

The volume of the wood block is given by V =
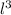`l^3`, where l is the length of one side of the block. Substituting the values, we get the expression for the buoyant force. Setting this equal to the weight of the wood block
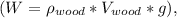`(W = $ \rho $_(wood) * V_(wood) * g),` we can solve for the distance the block is submerged (d) using Archimedes' principle.

`\[B = W\]`

`\[ \rho_(water) \cdot V_(water) \cdot g = \rho_(wood) \cdot V_(wood) \cdot g \]`

`\[ \rho_(water) \cdot l^3 \cdot g = \rho_(wood) \cdot l^3 \cdot g \]`

`\[ \rho_(water) = \rho_(wood) \]`

The density of the water is the same as the density of the wood, so half of the wood block is submerged. Therefore, the distance from the top of the block to the water is
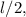`\( l/2 \),` which is 5.5 cm.