Question

Solve 12sin

2
(x)+2sin(x)−2=0 for all solutions 0≤x<2π x= Give your answers accurate to at least 3 decimal places, as a list separated by commas

Answer 1

The solutions to the equation 12sin²(x) + 2sin(x) - 2 = 0, where 0 ≤ x < 2π, accurate to at least 3 decimal places, are approximately x ≈ 0.339, 5.760.

To solve the equation 12sin²(x) + 2sin(x) - 2 = 0 for all solutions where 0 ≤ x < 2π, we can use the quadratic formula.

Let's treat sin(x) as a variable, say, y. The equation becomes a quadratic equation: 12y² + 2y - 2 = 0.

To solve this equation, we can use the quadratic formula: y = (-b ± √(b² - 4ac)) / (2a), where a = 12, b = 2, and c = -2.

Plugging in these values, we have:

y = (-2 ± √(2² - 4(12)(-2))) / (2(12))

= (-2 ± √(4 + 96)) / 24

= (-2 ± √100) / 24

= (-2 ± 10) / 24

Now, we have two possible solutions for y:

1) (-2 + 10) / 24 = 8 / 24 = 1/3

2) (-2 - 10) / 24 = -12 / 24 = -1/2

Since we set y = sin(x), we can solve for x by finding the inverse sine of each solution:

1) x =
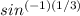`sin^((-1)(1/3))` ≈ 0.339 radians

2) x =
`sin^((-1)(-1/2))` ≈ -0.524 radians

However, we need to restrict the values of x to the interval 0 ≤ x < 2π. Since the second solution, -0.524 radians, is negative, we can add 2π to it to get the corresponding positive angle within the given interval:

2π + (-0.524) ≈ 5.760 radians.

Therefore, the solutions to the equation 12sin²(x) + 2sin(x) - 2 = 0, where 0 ≤ x < 2π, accurate to at least 3 decimal places, are approximately:

x ≈ 0.339, 5.760.

Answer 2

The value of x are 0.108,0.892, 3.309, 3.975 in radians or 19.5⁰, 160.5⁰, 210, 330 in degree.

How the values of x are determined.

Given

12sin²(x) + 2sin(x) - 2 = 0 for (0 <=x < 2π),

Factorise the equation

12sin²(x) + 6sin(x) -4sin(x) -2 = 0

6sin(x)(2sin(x) + 1)-2(2sinx + 1) = 0

(6sin(x) -2)(2sin(x) + 1) = 0

Equate each to zero

6sin(x) - 2 = 0 or 2sin(x) + 1 = 0

6sin(x) = 2 or 2sin(x) = -1

sin(x) = 2/6 or sin(x) = -1/2

sin(x) = 1/3 or sin(x) = -0.5

Find sine inverse of the expression

x = arcsin(1/3) or x = arcsin(-0.5)

Sine ratio is positive in the 1st and 2nd quadrant

x = 19.471 or 160.529

sine ratio is negative in 3rd and 4th quadrant.

x = arcsin (-0.5)

x = 330⁰ and 210⁰( in degree)

In radian

x = 0.108,0.892, 3.309, 3.975

In degree

19.5⁰, 160.5⁰, 210, 330

Complete question