Final answer:
To find the first terms and the explicit formula of an arithmetic sequence, one must use the arithmetic sequence formula, incorporating the given term and common difference to solve for the first term. The first term is then used to calculate the subsequent terms.
Step-by-step explanation:
Problem 1: Arithmetic Sequence
Given:
 = -276, d = -7
= -276, d = -7
To find: First five terms and explicit formula
Solution:
Find the first term (
 ):
):
 =
=
 - (36-1) × d = -276 - 35 × (-7) = -24
- (36-1) × d = -276 - 35 × (-7) = -24
Find the first five terms:
 = -24
= -24
 =
=
 + d = -31
+ d = -31
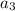 =
=
 + d = -38
+ d = -38
 =
=
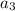 + d = -45
+ d = -45
 =
=
 + d = -52
+ d = -52
First five terms: -24, -31, -38, -45, -52
Explicit formula:
 =
=
 + (n-1) × d
+ (n-1) × d
 = -24 - 7(n-1)
= -24 - 7(n-1)
Problem 2: Geometric Series
Given: ∑(k=1 to 7) 4
To evaluate: The sum using the finite geometric sum formula
Solution:
Identify the values:
a = the first term = 4
r = the common ratio = 4 (since each term is 4 times the previous term)
n = the number of terms = 7
Apply the finite geometric sum formula:
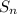 = a × (1 - rⁿ) / (1 - r)
= a × (1 - rⁿ) / (1 - r)
 = 4 × (1 - 4⁷) / (1 - 4) = 4 × (1 - 16384) / (-3) = 21844
= 4 × (1 - 4⁷) / (1 - 4) = 4 × (1 - 16384) / (-3) = 21844
Therefore, the sum of the series is 21844.