So, to maximize monthly revenue, the company should charge $9 per month, and the maximum revenue will be $121.5 million.
To maximize monthly revenue, we need to find the price at which the revenue is maximized. Revenue is calculated by multiplying the price per subscriber by the number of subscribers.
Let P be the price increase in dollars, and Q be the number of subscribers.
The original price is $8, and the original number of subscribers is 15 million.
So, the original revenue
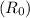 is given by:
is given by:
![\[ R_0 = P_0 * Q_0 = 8 * 15 \, \text{million} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nx4guctmbv893hb80wkyvirfkfz89o6wys.png)
Now, for each $1 increase in price, the company loses 1.5 million subscribers. So, if the price increases by P dollars, the number of subscribers Q will be
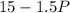 million.
million.
The revenue R with the price increase is given by:
![\[ R = (8 + P) * (15 - 1.5P) \, \text{million} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/f5q24vff5fffh1449aunqfo72kwheojzda.png)
Now, we want to find the value of P that maximizes R. To do this, we can find the critical points by taking the derivative of R with respect to P and setting it equal to zero:
![\[ (dR)/(dP) = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/q5c7c0sjxlzu3g3jdeebarqculp094mdx1.png)
![\[ (d)/(dP) [(8 + P) * (15 - 1.5P)] = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/c79rerm2jbz3engbn14lbz7bvgcdyh4loi.png)
![\[ (15 - 1.5P) - (8 + P) * 1.5 = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ix66txi4ozpvpblo84ecroj9732h7dddg7.png)
Sure, let's solve for P in the equation:
![\[ (15 - 1.5P) - (8 + P) * 1.5 = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ix66txi4ozpvpblo84ecroj9732h7dddg7.png)
First, distribute
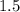 on the right side:
on the right side:
![\[ 15 - 1.5P - 12 - 1.5P = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ulf2j3rwlor1ktv8wzff8j0w4jwef60dh8.png)
Combine like terms:
![\[ 3 - 3P = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9epqnr1azsypkp1gkbkw5y0vi0jdbqlrug.png)
Now, isolate
 :
:
![\[ -3P = -3 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wmy9kneoqugrbwa7m7yi623ssv1gel52dn.png)
Divide both sides by
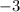 :
:
![\[ P = 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6xpplwzonqg7sq8su7snln2y6qlcjnp11g.png)
So,
 is the solution. Now, we need to determine the corresponding price and calculate the revenue.
is the solution. Now, we need to determine the corresponding price and calculate the revenue.
The original price is $8, and for each $1 increase, the new price is
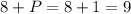 dollars.
dollars.
Now, calculate the revenue
 :
:
![\[ R = (8 + P) * (15 - 1.5P) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/el17bkqmrhvxmmfausr4hjm96pylxna8zt.png)
![\[ R = 9 * (15 - 1.5 * 1) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6u2xm72cpo0p82zpzi929r4d1va2pr5yz5.png)
![\[ R = 9 * 13.5 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/iuwjtswm9lqu7m76827vxshoa7szxkidqe.png)
![\[ R = 121.5 \, \text{million dollars} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dmt1wy2qmoir2g0rrx1n851ee3y8mqxect.png)