1. The equation of motion for the pendulum is:
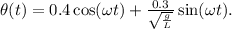
2. The period of the pendulum is
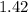 seconds.
seconds.
Solve the linear differential equation
 to find the equation of motion for the given initial conditions.
to find the equation of motion for the given initial conditions.
The general solution to this differential equation is
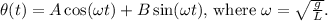
Given the initial conditions:
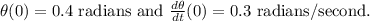
From the initial condition
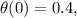 we get:
we get:
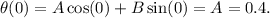
From the initial condition
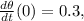 we derive the first derivative of
we derive the first derivative of
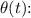
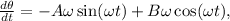
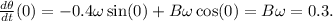
So,
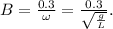
Therefore, the equation of motion for the pendulum is:
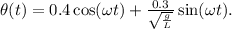
To find the period of the pendulum, the period
 is given by
is given by
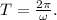
So,
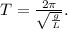
Given that
 and
and
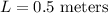 , we can compute the period:
, we can compute the period:
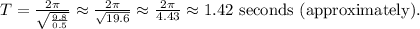
Therefore, the period of the pendulum is approximately
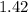 seconds.
seconds.
The complete question is here:
Suppose a pendulum of length L meters makes an angle of θ radians with the vertical, as in the figure. It can be shown that as a function of time, θ satisfies the differential equation
where
 is the acceleration due to gravity. For θ near zero we can use the linear approximation sin(θ)≈θ to get a linear differential equation
is the acceleration due to gravity. For θ near zero we can use the linear approximation sin(θ)≈θ to get a linear differential equation
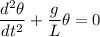
Use the linear differential equation to answer the following questions.
(a) Determine the equation of motion for a pendulum of length 0.5 meters having initial angle 0.4 radians and initial angular velocity
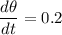 radians per second.
radians per second.
θ(t)= radians
(b) What is the period of the pendulum? That is, what is the time for one swing back and forth?