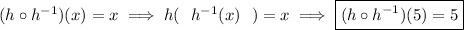Check the picture below.
we know that g(x) and h(x) are both one-to-one functions, so their inverse will also be a function, however let's recall that inverse functions have the original's domain as their range and the original's range as their domain, now a simpler way to say that, is the inverse function will be the same pairs as the original but flipped sideways, as you see in the picture, since we know that g(x) has (6 , 4) , then g⁻¹(x) will have the pair (4 , 6).
what's the inverse of h(x)?
as you already know, to get the inverse of any expression we start off by doing a quick switcheroo on the variables and then solving for "h", let's do so.
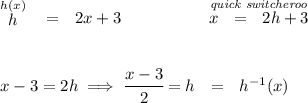
Now, another feature of invese functions is that, if we do a h( h⁻¹(x) ) the returned value is simply "x", what the heck does that mean? well it means