Question

Y to the power of 3 equals 8 what does y equal

Answer 1

`\displaystyle{y=2, -1\pm i√(3)}`

Explanation:

The polynomial
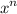`\displaystyle{x^n}` equation will have the number of "n" solutions. Therefore, when we're solving for:

`\displaystyle{y^3=8}`

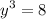
We're expecting to have 3 solutions. However, that generally applies in the complex set. Whereas, the real set is different and only have one solution, 2 or even 3 depending on the equation. See below for two methods:

Real Set (R)

By cube root both sides, we have:

`\displaystyle{\sqrt[3]{y^3}=\sqrt[3]{8}}`

Cancel the cube and evaluate the cube root of 8:

`\displaystyle{y=2}`

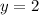
Therefore, y = 2 is the real solution.

Complex Set (C)

Subtract both sides by 8:

`\displaystyle{y^3-8=0}`

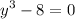
Apply the formula:

`\displaystyle{y^3-z^3=\left(y-z\right)\left(y^2+yz+z^2\right)}`

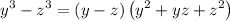
Therefore:

`\displaystyle{\left(y-2\right)\left(y^2+2y+4\right) = 0}\\\\\displaystyle{y = 2, y^2+2y+4=0}`

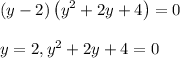
Solve the quadratic equation by quadratic formula:

`\displaystyle{y=(-b \pm √(b^2-4ac))/(2a)}\\\\\displaystyle{y=(-2\pm √(\left(-2\right)^2-4(1)(4) ))/(2(1))} \\\\\displaystyle{y = (-2\pm √(4-16))/(2) }\\\\\displaystyle{y=(-2\pm √(-12))/(2)}\\\\\displaystyle{y=(-2\pm 2i√(3))/(2)}\\\\\displaystyle{\therefore y = -1\pm i√(3)}`

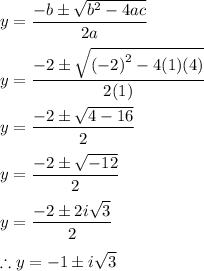
Therefore, within the complex set, the solutions are:

`\displaystyle{y=2, -1\pm i√(3)}`