Question

How many anagrams of TENTATIVE are there so that two T's are not adjacent?

Answer 1

12600

Explanation:

Solution 1: We can think of this problem as placing the non-T letters into a word first, then place the T’s in between the letters. In total, ENAIVE has
`(6!)/(2!)` total permutations. There are 7 gaps in between the letters, and we need to choose 3 of them to place our T’s, so there are a total of
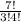`(7!)/(3!4!)` ways to do so (or more simply, seven choose 3), so our final outcome is
`(7!6!)/(2!3!4!)`. There are 12600 ways.

Solution 2: apply the Principle of inclusion-exclusion: Alternatively, what if we count what we don’t want? (Keep in mind, we have to subtract this amount from our total count to get the correct result, and the total amount of ways are 9!/2!3!) Rewording, our new problem is “in how many permutations of tentative are there at least two T’s together?” For this, we have to bring it case by case. If we can guarantee two T’s together, without regard to the 3rd T, there are 8*7!/2! Ways. With exactly 3, there are 7*6!/2! Ways. But in our first case, we overcounted three T’s twice, so we have to subtract our 2nd result from the first result. In total, there are 12600 ways.