Question

Use Technology to find the p-Yalue for the claim H1:μ<76, if the test statistic is known to be t=−1,45 and n=81. Will the test statistic, t=−1.45 be the upper or lower bound for a left tail test? A. Upper bound, since we want the area to the lat of this value for a left tail. B. Lower bound, sinee we want the area to the right of this value for a left tail. What Is the p-value?

Answer 1

a. Left-tail test is 0.0027.

b. p-value is 80 degree.

The question is asking for the p-value corresponding to a chi-square (χ²) statistic for a left-tail test. Given the test statistic (χ² = 49.32) and the sample size (n = 81), we can calculate the p-value using the chi-square distribution.

For a left-tail test:

• The null hypothesis H0 is that the true variance is greater than or equal to some value.
• The alternative hypothesis H1 is that the true variance is less than that value.

Given that H1 is that the true variance is less than the claimed value, and since we're looking at a left-tail test, we're interested in the area to the left of the test statistic on the chi-square distribution.

The steps to find the p-value are as follows:

1. Determine the degrees of freedom for the test, which is n - 1.

2. Use the chi-square distribution with the determined degrees of freedom to find the area to the left of the test statistic χ² = 49.32.

3. This area is the p-value.

Let's perform the calculation. We'll find the degrees of freedom first and then calculate the p-value.

The p-value for the given chi-square statistic of 49.32 with 80 degrees of freedom (since
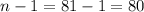`\( n - 1 = 81 - 1 = 80 \)`) in a left-tail test is 0.0027 when rounded to four decimal places.

Answer 2

The test statistic would be the Upper bound since we want the area to the left of this value for a left tail. The Pvalue is 0.0754

Using the parameters given for our Calculation;

• test statistic = -1.45
• sample size, n = 81

The Null and Alternative hypothesis;

• 
  `H_(0) : μ > 76`
• 
  `H_(1) : μ < 76`

Since the value of the test statistic is negative, Then we want the left tailed value to the left .

Using the P - value calculator :

• Pvalue(test statistic, df = n-1)

Pvalue(-1.45, 80) at 0.05 level of significance is 0.0754

Since, the Pvalue > 0.05, Then the result is not significant at 0.05.