Question

Line g has a slope of 4 and passes through point (-2,6). What is the equation for the line in slope-intercept form?

Answer 1

`\bullet\qquad\mathbf{y=4x+14}`

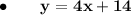
Detailed explanation:

Hi there! Our task is to find the equation of line g, given that :-

✦ its slope is 4

✦ it passes through a point (-2,6)

I am going to write the equation in Point - Slope form :-

`\rightleftharpoons\qquad\mathbf{y-y_1=m(x-x_1)}`

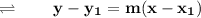
Where :-

• 
  `\mathbf{y_1=the~y-coordinate~of~the~point}`
• 
  `\mathbf{m=slope}`
• 
  `\mathbf{x_1=the~x-coordinate~of~the~point}`

Plug in the data :-

`\stackrel{\diamond}{\boxed{\boxed{\begin{gathered}\leadsto\mathbf{y-6=4(x-(-2)}\\\leadsto\mathbf{y-6=4(x+2)}\\\leadsto\mathbf{y-6=4x+8} \\\leadsto\mathbf{y=4x+8+6}\\\leadsto\mathbf{y=4x+14}\end{gathered}}}}`

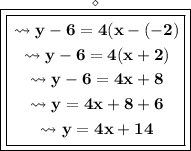
`\bigstar` Therefore, the equation is y = 4x + 14.

====

Have an awesome day!

====

Answer 2

• C) y = 4x + 14

-----------------------

Use the point-slope form:

• y - y₁ = m(x - x₁), where m is the slope and (x₁, y₁) is the point on the line

Substitute the value of the slope and coordinates to get:

• y - 6 = 4(x - (-2))

Convert this into slope-intercept form of y = mx + b:

• y - 6 = 4x + 8
• y = 4x + 8 + 6
• y = 4x + 14