Answer:
Approximately
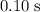 (assuming that
(assuming that
 and that air resistance is negligible.)
and that air resistance is negligible.)
Step-by-step explanation:
Assume that before the ruler was released, the person whose reaction time is being measured initially placed their hand at the lower end of the ruler. Since the ruler would be in a free fall while the person has yet to react, the reaction time of the person can be calculated from the distance that ruler has travelled.
During the free fall, the ruler started from rest (initial velocity of
 ) and accelerates at a constant
) and accelerates at a constant
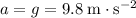 . The following SUVAT equation models the displacement
. The following SUVAT equation models the displacement
 of the ruler at time
of the ruler at time
 :
:
 .
.
Since
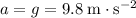 and
and
 , this equation becomes:
, this equation becomes:
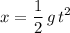 .
.
Given that
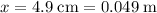 (note the unit conversion,) rearrange this equation to find the amount of time
(note the unit conversion,) rearrange this equation to find the amount of time
 the ruler was in a free fall:
the ruler was in a free fall:
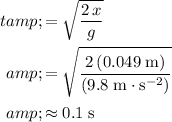 .
.
Therefore, the reaction time of this person would be
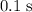 .
.