Question

Quick answer fast please

Answer 1

x = 4

Explanation:

To solve the given equation for "x," we can use the properties of exponents.

Here is a table of exponent rules you can use:

`\boxed{\left\begin{array}{ccc}\text{\underline{Exponent rules:}}\\\\1.\ a^0=1\\\\2.\ a^m * a^n=a^(m+n)\\\\3.\ a^m / a^n=a^(m-n)\\\\4.\ (ab)^m=a^mb^m\\\\5.\ (a/b)^m=a^m/b^m\\\\6.\ (a^m)^n=a^(mn)\\\\7.\ a^(-m)=1/a^m\\\\8.\ a^(m/n)=(\sqrt[n]{a} )^m\end{array}\right}\\\\\\\hrule`

Now answering,

First, let's simplify the left side of the equation. When dividing two numbers with the same base, we subtract the exponents (rule #3). In this case, we have:

`(7^7)/(7^3)=7^x \rightarrow 7^(7-3)=7^x \rightarrow \boxed{7^4=7^x}`

So the equation simplifies to
`7^4=7^x`.

Now, we can solve for "x" by equating the exponents. Since the bases are the same, the exponents must be equal. Therefore, we have:

`4=x \rightarrow \boxed{\boxed{x=4}}`

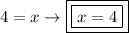
Alternatively, we can take the natural logarithm of both sides of the equation,
`7^4=7^x`.

`7^4=7^x \rightarrow \ln(7^4)= \ln(7^x) \rightarrow 4 \ln(7)= x \ln(7) \rightarrow \boxed{\boxed{x=4}}`

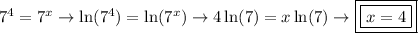
Hence, the solution to the equation is x = 4.