Question

Claim: The mean systolic blood pressure of all healthy adults is less than than 124 mmHg. Sample data: For 299 healthy adults, the mean systolic blood pressure level is 123.81 mmHg and the standard deviation is 16.01 mmHg. The null and alternative hypotheses are H

0
​
:μ=124 and H
1
​
: μ<124. Find the value of the test statistic.

Answer 1

The value of the test statistic is approximately -0.044.

Step-by-step explanation:

To find the value of the test statistic, we first need to calculate the z-score for the sample mean using the formula:

z = (x - μ) / (σ /
`√(n)`)

where x is the sample mean, μ is the population mean, σ is the standard deviation, and n is the sample size. In this case, x = 123.81 mmHg, μ = 124 mmHg, σ = 16.01 mmHg, and n = 299. Plugging in these values, we get:

z = (123.81 - 124) / (16.01 /
`√(299)`)

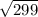Simplifying the equation, we find that z ≈ -0.044. Therefore, the value of the test statistic is approximately -0.044.