The number of turns in the solenoid is approximately 28,937 turns.
How to determine the number of turns the solenoid must have?
The magnetic field within a solenoid is represented by the formula
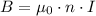 , where
, where
 is the magnetic field strength,
is the magnetic field strength,
 is the permeability of free space,
is the permeability of free space,
 stands for the number of turns in the solenoid, and
stands for the number of turns in the solenoid, and
 denotes the current passing through the coil.
denotes the current passing through the coil.
Given a magnetic field strength
 , and the length of the solenoid
, and the length of the solenoid
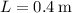 , we can determine the number of turns
, we can determine the number of turns
 using the formula
using the formula
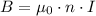 .
.
By rearranging the formula and solving for
 , we find:
, we find:
![\[ n = (B \cdot L)/(\mu_0 \cdot I) \]](https://img.qammunity.org/2024/formulas/physics/high-school/5vm7jx783zdktoyq6ap5i0pv1k16q4euvl.png)
Substituting the given values:
![\[ n = \frac{0.40 \, \text{T} \cdot 0.4 \, \text{m}}{\mu_0 \cdot 4.4 \, \text{A}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/hovnryxxhmt057nrw1h8zqcduq96x9jc6d.png)
The value of
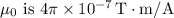 .
.
![\[ n = (0.4 \cdot 0.4)/(4\pi * 10^(-7) \cdot 4.4) \]](https://img.qammunity.org/2024/formulas/physics/high-school/wpwlmamgzxmhaw7s6u6aoevk8ecpdha13h.png)
Calculating this yields approximately 28,937.3 turns.
Therefore, the number of turns in the solenoid is approximately 28,937 turns.