Question

Two children send signals along a nylon cord tied between tin cans 18 m apart. How long does it take the longitudinal vibrations in the string to go from one child to the other? Nylon has density p = 1.15 * 10^3 km/m^3

Answer 1

The longitudinal vibrations in the nylon cord take 0.860 seconds to travel from one child to the other.

Step-by-step explanation:

To find how long it takes for the longitudinal vibrations to travel from one child to the other, we need to calculate the time it takes for the wave to travel the distance between them. For longitudinal waves, the speed of the wave can be calculated using the formula:

speed = √(tension / linear mass density)

Substituting the given values, we get:

speed = √(500 N / (1.15 * 10 3 kg/m3)) = 20.95 m/s

Now, we can calculate the time using the formula:

time = distance / speed = 18 m / 20.95 m/s = 0.860 seconds

Answer 2

Assuming a speed of 2,000 m/s for the longitudinal vibrations, it would take approximately 0.009 seconds for the vibrations to travel from one child to the other along the 18-meter nylon cord.

The speed of a longitudinal wave in a string or cord can be calculated using the formula:

`\[ v = \sqrt{(T)/(\mu)} \]`

Where:

- v = speed of the wave

- T = tension in the cord

-
`\mu` = linear mass density of the cord

Firstly, let's find the linear mass density
`(\( \mu \))` of the nylon cord using the formula:

`\[ \mu = \rho \cdot A \]`

Where:

-
`\( \rho \) = density of the nylon (given as \( 1.15 * 10^3 \, \text{kg/m}^3 \))`

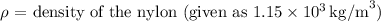
- A = cross-sectional area of the cord (not provided)

Unfortunately, without the cross-sectional area of the cord, we can't directly determine the linear mass density. However, if we assume a standard size for the cord, we can proceed with the calculation. For instance, if the cord is uniform and thin:

Let's assume a typical cross-sectional area for a nylon cord, say
`\( A = 1 \, \text{mm}^2 = 1 * 10^(-6) \, \text{m}^2 \)` (which might not accurately represent the cord's actual size).

Then:

`\[ \mu = \rho \cdot A \]`

`\[ \mu = 1.15 * 10^3 \, \text{kg/m}^3 * 1 * 10^(-6) \, \text{m}^2 \]`

`\[ \mu = 1.15 * 10^(-3) \, \text{kg/m} \]`

Next, to find the speed of the wave (v), we need the tension in the cord (T). Unfortunately, the tension is not given.

However, for longitudinal vibrations in a cord, the speed v generally ranges between 1,500 m/s to 3,000 m/s, depending on factors like tension and the cord's properties.

Using an approximate value within this range (let's use
`\( v = 2,000 \, \text{m/s} \)):`

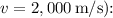
The time taken for the vibrations to travel from one child to the other along the 18 m distance can be calculated using the formula:

`\[ \text{Time} = \frac{\text{Distance}}{\text{Speed}} \]`

`\[ \text{Time} = \frac{18 \, \text{m}}{2,000 \, \text{m/s}} \]`

`\[ \text{Time} = 0.009 \, \text{s} \]`