Question

The function f is defined by f(x)=2x-1/x+1​

Answer 1

`\begin{aligned}\textsf{(a)}\textsf{(i)}\quad x &= -1\\\textsf{(ii)} \quad y &= 2\end{aligned}`

`\textsf{(b)} \qquad \sf See\;attached\;graph.`

`\textsf{(c)} \qquad x > (1)/(2)`

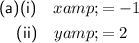
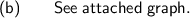
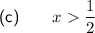
Explanation:

A rational function f is defined by:

`f(x)=(2x-1)/(x+1), \;\;\text{where}\;x \in \mathbb{R}, x \\eq -1`

`\hrulefill`

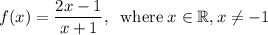
Part (a)

An asymptote is a line that the curve gets infinitely close to, but never touches.

To find the vertical asymptote(s) of a rational function, set the denominator to zero and solve for x:

`x+1=0 \implies x=-1`

Therefore, the vertical asymptote is x = -1.

Horizontal Asymptotes:

• If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is y = 0.
• If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote (but there is a slant asymptote).
• If the degree of the numerator is equal to the degree of the denominator, divide the highest degree term of the numerator by the highest degree term of the denominator.

As the degree of the numerator of the given function is equal to the degree of the denominator of the given function, the horizontal asymptote is:

`y=(2x)/(x)=2`

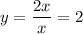
Therefore, the horizontal asymptote is y = 2.

`\hrulefill`

Part (b)

To find the x-intercept(s) of the function, set the function to zero and solve for x:

`\begin{aligned}(2x-1)/(x+1)&=0\\\\2x-1&=0\\\\2x&=1\\\\x&=(1)/(2)\end{aligned}`

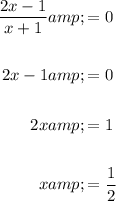
Therefore, the x-intercept is (1/2, 0).

To find the y-intercept of the function, substitute x = 0 into the function and solve for y:

`\begin{aligned}x=0 \implies y&=(2(0)-1)/(0+1)\\\\y&=(0-1)/(1)\\\\y&=-1\end{aligned}`

Therefore, the y-intercept is (0, -1).

To sketch the graph of y = f(x):

• Draw the asymptotes y = 2 and x = -1 as dashed lines.
• Draw a continuous curve in quadrant II that is above the asymptote y = 2 and to the left of the asymptote x = -1. The curve approaches y = 2 as x tends to -∞, and approaches +∞ as x tends to x = -1.
• Draw a continuous curve that starts in quadrant III on the right side of the asymptote x = -1, passes through (0, -1) and (1/2, 0) and approaches the asymptote y = 2 as x tends to +∞.

`\hrulefill`

Part (c)

To solve the inequality 0 < f(x) < 2, observe the x-values of the curve between f(x) = 0 and f(x) = 2.

When f(x) = 0, x = 1/2.

The curve never reaches f(x) = 2 as there is an asymptote at y = 2.

Therefore, the solution to the inequality is x > 1/2.