Question

Please help with this question

Answer 1

`\displaystyle \int\limits^(-1)_(-2) {\int\limits^(5)_(3) {\int\limits^(-1)_(-2) {2xy^2} \, dx } \, dy } \, dz = \boxed{-(392)/(3) }`

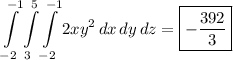
Explanation:

Evaluate the given triple-integral over the region "B."

`\displaystyle \iiint_B 2xy^2 dV\\\\B=\ -2\leq x\leq 0, \ 3\leq y\leq 5, \ -2\leq z\leq -1\\\\\\hrule`

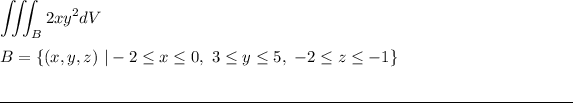
Part (a) - Set up the integral.

Setting up the integral we get:

`\Longrightarrow \displaystyle \int\limits^(-1)_(-2) {\int\limits^(5)_(3) {\int\limits^(0)_(-2) {2xy^2} \, dx } \, dy } \, dz`

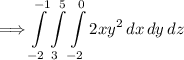
Part (b) - Evaluate the integral.

Utilizing the power rule for integration, we can integrate this integral.

`\Longrightarrow \displaystyle \int\limits^(-1)_(-2) {\int\limits^(5)_(3) {\int\limits^(0)_(-2) {2xy^2} \, dx } \, dy } \, dz`

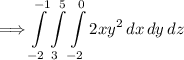
First, integrating with respect to "x." This means we will treat all other variables as constants.

`\Longrightarrow \displaystyle \int\limits^(-1)_(-2) {\int\limits^(5)_(3) {\int\limits^(0)_(-2) {2xy^2} \, dx } \, dy } \, dz\\\\\\\\\Longrightarrow \displaystyle 2y^2\int\limits^(-1)_(-2) {\int\limits^(5)_(3) {\int\limits^(0)_(-2) {x} \, dx } \, dy } \, dz\\\\\\\\\Longrightarrow \displaystyle 2y^2\int\limits^(-1)_(-2) {\int\limits^(5)_(3) {\Big[(1)/(2) x^2 \Big]\limits^(0)_(-2)} \, dy } \, dz\\\\\\\\`

`\Longrightarrow \displaystyle 2y^2\int\limits^(-1)_(-2) {\int\limits^(5)_(3) {\Big[(1)/(2) (0)^2 - (1)/(2)(-2)^2 \Big]} \, dy } \, dz\\\\\\\\\Longrightarrow \displaystyle 2y^2\int\limits^(-1)_(-2) {\int\limits^(5)_(3) {\Big[(1)/(2) (0) - (1)/(2)(4) \Big]} \, dy } \, dz\\\\\\\\\Longrightarrow \displaystyle 2y^2\int\limits^(-1)_(-2) {\int\limits^(5)_(3) {\Big[0 - 2 \Big]} \, dy } \, dz\\\\\\\\`

`\Longrightarrow \displaystyle 2y^2\int\limits^(-1)_(-2) {\int\limits^(5)_(3) {\Big[-2 \Big]} \, dy } \, dz\\\\\\\\\Longrightarrow \displaystyle 2 \cdot -2\int\limits^(-1)_(-2) {\int\limits^(5)_(3) {y^2} \, dy } \, dz\\\\\\\\\boxed{\Longrightarrow \displaystyle -4 \int\limits^(-1)_(-2) {\int\limits^(5)_(3) {y^2} \, dy } \, dz}`

Next, integrating with respect to the variable "y."

`\Longrightarrow \displaystyle -4 \int\limits^(-1)_(-2) {\int\limits^(5)_(3) {y^2} \, dy } \, dz\\\\\\\\\Longrightarrow \displaystyle -4 \int\limits^(-1)_(-2) { {\Big[(1)/(3)y^3\Big]\limits^(5)_(3)} \, } \, dz\\\\\\\\\Longrightarrow \displaystyle -4 \int\limits^(-1)_(-2) { {\Big[(1)/(3)(5)^3-(1)/(3)(3)^3\Big]} \, } \, dz\\\\\\\\\Longrightarrow \displaystyle -4 \int\limits^(-1)_(-2) { {\Big[(1)/(3)(125)-(1)/(3)(27)\Big]} \, } \, dz\\\\\\\\`

`\Longrightarrow \displaystyle -4 \int\limits^(-1)_(-2) { {\Big[(125)/(3)-9\Big]} \, } \, dz\\\\\\\\\Longrightarrow \displaystyle -4 \int\limits^(-1)_(-2) { {(98)/(3)} \, } \, dz\\\\\\\\\Longrightarrow \displaystyle - 4 \cdot(98)/(3)\int\limits^(-1)_(-2) { {1} \, } \, dz\\\\\\\\\Longrightarrow \boxed{\displaystyle - (392)/(3)\int\limits^(-1)_(-2) { {1} \, } \, dz}`

Lastly, integrating with respect to the variable "z." We will utilize the constant rule for integration.

`\Longrightarrow \displaystyle - (392)/(3) \int\limits^(-1)_(-2) { {1} \, } \, dz\\\\\\\ \Longrightarrow -(392)/(3) \Big[z\Big]\limits^(-1)_(-2)\\\\\\\\\Longrightarrow -(392)/(3) \Big[-1-(-2)\Big]\\\\\\\\\Longrightarrow -(392)/(3) \Big[-1+2\Big]\\\\\\\\\Longrightarrow -(392)/(3) (1)\\\\\\\\\therefore \boxed{\boxed{-(392)/(3) }}`

Thus, the problem is solved.
`\hrulefill`

Integration rules used:

`\boxed{\left\begin{array}{ccc}\text{\underline{Power Rule:}}\\\\\displaystyle \int x^n \ dx = (x^(n+1))/(n+1) \end{array}\right }`

`\boxed{\left\begin{array}{ccc}\text{\underline{Constant Rule:}}\\\\\displaystyle \int a\ dx = ax\end{array}\right }`