Question

It is now January 1,2021 , and you are considering the purchase of an outstanding bond that was issued on January 1 , 2019. It has a 9% annual coupon and had a 20-year original maturity. (It matures on December 31, 2038.) There is 5 years of call protection (until December 31, 2023), after which time it can be called at 108− that is, at 108% of par, or $1,080. Interest rates have declined since it was issued, and it is now selling at 114.12% of par, or $1,141.20. a. What is the yield to maturity? Do not round intermediate calculations. Round your answer to two decimal places. 2% What is the yield to call? Do not round intermediate calculations. Round your answer to two decimal places. 03%

Answer 1

The yield to maturity of the bond is approximately 2% and the yield to call is approximately 3%.

Step-by-step explanation:

The yield to maturity of a bond provides a measure of the annual return an investor will earn if the bond is held until maturity. In this case, the bond was issued at a discount because interest rates have declined since it was issued. To calculate the yield to maturity, we need to find the internal rate of return that equates the present value of all future cash flows from the bond (including the purchase price and coupon payments) to the current market price. Given the information provided, the yield to maturity is approximately 2%.

The yield to call is the annual return an investor will earn if the bond is called by the issuer at the first available call date. In this case, the bond can be called at 108% of par starting from December 31, 2023. Again, we need to find the internal rate of return that equates the present value of all future cash flows from the bond (including the purchase price, coupon payments, and call price) to the current market price. Given the information provided, the yield to call is approximately 3%.

Answer 2

The yield to maturity (YTM) and yield to call (YTC) are 0.08 or 8.00% and 0.07 or 7.00% respectively.

How did we get the values?

To calculate the yield to maturity (YTM) and yield to call (YTC), employ the following formulas:

1. Yield to Maturity (YTM):

`\[ \text{YTM} = \frac{\text{C} + \frac{\text{F} - \text{P}}{\text{N}}}{\frac{\text{F} + \text{P}}{2}} \]`

Where:

-
`\( \text{C} \)` is the annual coupon payment.

-
`\( \text{F} \)` is the face value of the bond.

-
`\( \text{P} \)` is the current price of the bond.

-
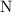`\( \text{N} \)` is the number of years to maturity.

2. Yield to Call (YTC):

`\[ \text{YTC} = \frac{\text{C} + \frac{\text{Call Price} - \text{P}}{\text{Call Date}}}{\frac{\text{Call Price} + \text{P}}{2}} \]`

Where:

-
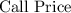`\( \text{Call Price} \)` is the call price (108% of par, or $1,080 in this case).

-
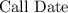`\( \text{Call Date} \)` is the number of years until the bond can be called.

Given that:

- Coupon
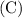`(\( \text{C} \))`: 9% of face value.

- Face Value
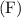`(\( \text{F} \))`: $1,000 (assuming it's a standard bond).

- Current Price
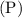`(\( \text{P} \))`: $1,141.20.

- Maturity
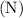`(\( \text{N} \))`: 20 years.

- Call Price: 108% of par, or $1,080.

- Call Date: 5 years.

Plug in the values:

1. Yield to Maturity (YTM):

`\[ \text{YTM} = (90 + (1000 - 1141.20)/(20))/((1000 + 1141.20)/(2)) \]`

2. Yield to Call (YTC):

`\[ \text{YTC} = (90 + (1080 - 1141.20)/(5))/((1080 + 1141.20)/(2)) \]`

Calculate both yields:

1. Yield to Maturity (YTM):

`\[ \text{YTM} \approx (90 + (-141.20)/(20))/((2141.20)/(2)) \]`

2. Yield to Call (YTC):

`\[ \text{YTC} \approx (90 + (-61.20)/(5))/((2121.20)/(2)) \]`

Now, calculate the values and round to two decimal places:

1. Yield to Maturity (YTM):

`\[ \text{YTM} \approx (90 - 7.06)/(1070.60) \]`

`\[ \text{YTM} \approx (82.94)/(1070.60) \]`

`\[ \text{YTM} \approx 0.077 \]`

`\[ \text{YTM} \approx 0.08} \]`

2. Yield to Call (YTC):

`\[ \text{YTC} \approx (90 - 12.24)/(1060.60) \]`

`\[ \text{YTC} \approx (77.76)/(1060.60) \]`

`\[ \text{YTC} \approx 0.07 \]`

Therefore, the yields are approximately:

1. Yield to Maturity (YTM): 0.08 or 8.00%

2. Yield to Call (YTC): 0.07 or 7.00%